题目内容
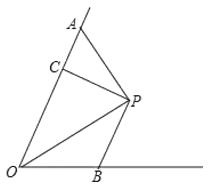
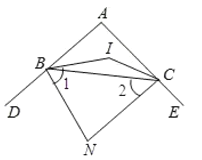
【题目】△ABC中，∠A=100°，BI、CI分别平分∠ABC，∠ACB，则∠BIC=________；若BN、CN分别平分∠ABC，∠ACB的外角，则∠N=_________
【答案】140° 40°
【解析】
首先根据三角形内角和定理求出∠ABC＋∠ACB的度数，再根据角平分线的性质得到∠IBC＝
∠ABC，∠ICB＝∠ACB，求出∠IBC＋∠ICB的度数，再次根据三角形内角和定理求出∠BIC的度数即可；
根据∠ABC＋∠ACB的度数，算出∠DBC＋∠ECB的度数，然后再利用角平分线的性质得到∠1＝∠DBC，∠2＝ECB，可得到∠1＋∠2的度数，最后再利用三角形内角和定理计算出∠N的度数．
解：如图，
∵∠A＝100°，
∵∠ABC＋∠ACB＝180°100°＝80°，
∵BI、CI分别平分∠ABC，∠ACB，
∴∠IBC＝∠ABC，∠ICB＝∠ACB，
∴∠IBC＋∠ICB＝∠ABC＋∠ACB＝（∠ABC＋∠ACB）＝×80°＝40°，
∴∠BIC＝180°（∠IBC＋∠ICB）＝180°40°＝140°；
∵∠ABC＋∠ACB＝80°，
∴∠DBC＋∠ECB＝360°（∠ABC＋∠ACB）＝360°80°＝280°，
∵BN、CN分别平分∠ABC，∠ACB的外角，
∴∠1＝∠DBC，∠2＝∠ECB，
∴∠1＋∠2＝×280°＝140°，
∴∠N＝180°(∠1+∠2)＝40°．
故答案为：140°，40°．
【题目】某公司根据市场计划调整投资策略，对A、B两种产品进行市场调查，收集数据如下表：
项目 产品 | 年固定成本 （单位：万元） | 每件成本 （单位：万元） | 每件产品销售价 （万元） | 每年最多可生产的件数 |
A | 20 | m | 10 | 200 |
B | 40 | 8 | 18 | 120 |
其中，m是待定系数，其值是由生产A的材料的市场价格决定的，变化范围是6≤m＜8，销售B产品时需缴纳
x2万元的关税．其中，x为生产产品的件数．假定所有产品都能在当年售出，设生产A，B两种产品的年利润分别为y1、y2（万元）．
（1）写出y1、y2与x之间的函数关系式，注明其自变量x的取值范围．
（2）请你通过计算比较，该公司生产哪一种产品可使最大年利润更大？
