题目内容
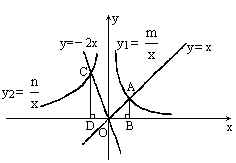
如图所示,正比例函数y=x和y=-2x的图像分别与双曲线y1=![]() 和y2=
和y2=![]() (mn≠0)相交于A,C两点,若Rt△OCD的面积是Rt△OAB的面积的两倍,问点P(m,n)是否在函数y=-2x上?说明理由.
(mn≠0)相交于A,C两点,若Rt△OCD的面积是Rt△OAB的面积的两倍,问点P(m,n)是否在函数y=-2x上?说明理由.
答案:
解析:
解析:
|
点 P(m,n)在直线y=-2x上,理由如下:设B(a,0),D(b,0),则A(a,a),C(-b,-2b),OB=|a|=a,OD=|b|=-b.AB=|a|=a,CD=|-2b|=-2b.S△COD= |

练习册系列答案
相关题目
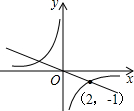 如图所示,正比例函数y=k1x与反比例函数y=
如图所示,正比例函数y=k1x与反比例函数y=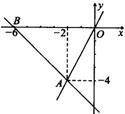 13、如图所示,正比例函数y1=kx与一次函数y2=-x+a的图象交于点A,根据图上给出的条件,回答下列问题:
13、如图所示,正比例函数y1=kx与一次函数y2=-x+a的图象交于点A,根据图上给出的条件,回答下列问题: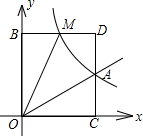 已知:如图所示,正比例函数y=ax的图象与反比例函数y=
已知:如图所示,正比例函数y=ax的图象与反比例函数y= 如图所示,正比例函数y=kx(k>0)与反比例函数y=
如图所示,正比例函数y=kx(k>0)与反比例函数y=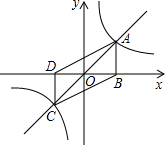 如图所示,正比例函数y=x与反比例函数
如图所示,正比例函数y=x与反比例函数