题目内容
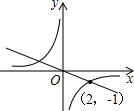如图所示，正比例函数y=k1x与反比例函数y=| k2 | x |
分析：反比例函数的图象是中心对称图形，则与经过原点的直线的两个交点一定关于原点对称．
解答：解：由图象可知：直线y=k1x经过原点与双曲线y=
相交于两点，
又由于双曲线y=
与直线y=mx均关于原点对称．
则两点关于原点对称，一个交点的坐标为（2，-1），
则另一个交点的坐标为（-2，1）．
故答案为：（-2，1）．
| k2 |
| x |
又由于双曲线y=
| k2 |
| x |
则两点关于原点对称，一个交点的坐标为（2，-1），
则另一个交点的坐标为（-2，1）．
故答案为：（-2，1）．
点评：本题考查反比例函数图象的中心对称性，即两点关于原点对称．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
13、如图所示，正比例函数y1=kx与一次函数y2=-x+a的图象交于点A，根据图上给出的条件，回答下列问题：
已知：如图所示，正比例函数y=ax的图象与反比例函数y=
如图所示，正比例函数y=kx（k＞0）与反比例函数y=
如图所示，正比例函数y=x与反比例函数