题目内容
 已知:如图所示,正比例函数y=ax的图象与反比例函数y=
已知:如图所示,正比例函数y=ax的图象与反比例函数y=| k | x |
(1)试确定上述正比例函数和反比例函数的表达式;
(2)M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,求M点坐标.
分析:(1)由点A为正比例与反比例函数图象的交点,将A点坐标代入正比例函数y=ax中,求出a的值,确定出正比例函数的解析式,将A点坐标代入反比例函数y=
中,求出k的值,确定出反比例函数的解析式;
(2)过M作MN垂直于x轴,由M为反比例函数上的点,将M的坐标代入反比例函数解析式中求出mn=6,同时由三个角为直角的四边形为矩形,得到四边形BOCD为矩形,根据矩形的对边相等可得出BO=DC,又BMNO为矩形,得到MN=BO,由M的纵坐标为n,得到MN=BO=DC=n,横坐标为m,得到BM=m,由A的坐标得出AC及OC的长,四边形OADM的面积=矩形BOCD的面积-三角形BMO的面积-三角形AOC的面积,利用矩形及三角形的面积公式分别表示出各自的面积,将mn=6及四边形OADM的面积为6代入,得出关于n的方程,求出方程的解得到n的值,进而求出m的值,即可确定出M的坐标.
| k |
| x |
(2)过M作MN垂直于x轴,由M为反比例函数上的点,将M的坐标代入反比例函数解析式中求出mn=6,同时由三个角为直角的四边形为矩形,得到四边形BOCD为矩形,根据矩形的对边相等可得出BO=DC,又BMNO为矩形,得到MN=BO,由M的纵坐标为n,得到MN=BO=DC=n,横坐标为m,得到BM=m,由A的坐标得出AC及OC的长,四边形OADM的面积=矩形BOCD的面积-三角形BMO的面积-三角形AOC的面积,利用矩形及三角形的面积公式分别表示出各自的面积,将mn=6及四边形OADM的面积为6代入,得出关于n的方程,求出方程的解得到n的值,进而求出m的值,即可确定出M的坐标.
解答:解:(1)∵点A(3,2)为正比例函数与反比例函数的交点,
∴将x=3,y=2代入正比例解析式y=ax得:3a=2,解得:a=
,
将x=3,y=2代入反比例解析式y=
得:
=2,解得:k=6,
∴正比例函数解析式为y=
x,反比例函数解析式为y=
;
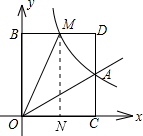
(2)过M作MN⊥x轴于N点.
∵M(m,n)(0<m<3)是反比例函数图象上的一动点,且四边形OCDB为矩形,
∴mn=6,BM=m,BO=DC=MN=n,
又A(3,2),
∴AC=2,OC=3,又mn=6,
∴S四边形OADM=S矩形OCDB-S△BMO-S△AOC=3n-
mn-
×2×3=3n-6=6,
解得:n=4,
由mn=6,得到4m=6,解得:m=
,
则M坐标为(
,4).
∴将x=3,y=2代入正比例解析式y=ax得:3a=2,解得:a=
| 2 |
| 3 |
将x=3,y=2代入反比例解析式y=
| k |
| x |
| k |
| 3 |
∴正比例函数解析式为y=
| 2 |
| 3 |
| 6 |
| x |

(2)过M作MN⊥x轴于N点.
∵M(m,n)(0<m<3)是反比例函数图象上的一动点,且四边形OCDB为矩形,
∴mn=6,BM=m,BO=DC=MN=n,
又A(3,2),
∴AC=2,OC=3,又mn=6,
∴S四边形OADM=S矩形OCDB-S△BMO-S△AOC=3n-
| 1 |
| 2 |
| 1 |
| 2 |
解得:n=4,
由mn=6,得到4m=6,解得:m=
| 3 |
| 2 |
则M坐标为(
| 3 |
| 2 |
点评:此题属于反比例函数的综合题,涉及的知识有:反比例函数与一次函数的交点,矩形的判定与性质,以及点与坐标的关系,利用了数形结合及方程的思想,是中考中常考的题型.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
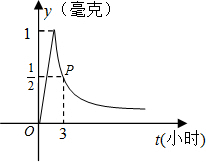 教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?
教室,那么从药物释放开始,至少需要经过多少小时后,学生才能进入教室?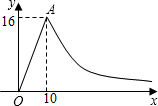 药量为16mg.根据以上信息解答下列问题:
药量为16mg.根据以上信息解答下列问题: 要经过多少小时后,学生才能进入教室?
要经过多少小时后,学生才能进入教室? 为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y=
为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒,已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为y= 为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为
为了预防流感,某学校在休息天用药熏消毒法对教室进行消毒.已知药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间t(小时)成正比;药物释放完毕后,y与t的函数关系式为