题目内容
【题目】如图,在正方形![]() 中
中![]() 与
与![]() 交于点
交于点![]() 形外有一点
形外有一点![]() ,使
,使![]() ,且
,且![]() ,则
,则![]() _____.
_____.

【答案】![]()
【解析】
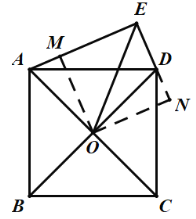
过点O作OM⊥AE,ON⊥ED,则四边形OMEN是矩形,则∠MON=90°,然后证明△AOM≌△DON,得到AM=DN,OM=ON,则矩形OMEN是正方形,由![]() ,求出ME=4,然后求出AM=DN=1,即可得到答案.
,求出ME=4,然后求出AM=DN=1,即可得到答案.
解:如图:过点O作OM⊥AE,ON⊥ED,
∴∠OME=90°,∠ONE=90°,
∵![]() ,
,
∴四边形OMEN是矩形,
∴∠MON=90°,
在正方形ABCD中,OA=OD,∠AOD=90°,
∴∠AOM+∠MOD=∠MOD+∠DON=90°,
∴∠AOM=∠DON,
∵∠AMO=∠DNO,
∴△AOM≌△DON,
∴AM=DN,OM=ON,
∴四边形OMEN是正方形,
设ME=MO=EN=x,![]() ,由勾股定理得:
,由勾股定理得:
![]() ,
,
解得:![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ;
;
故答案为:5.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目