题目内容
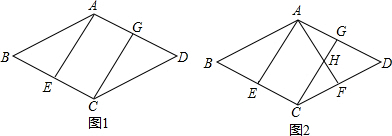
已知:如图(1)菱形ABCD的边长为4,∠ADC=120°,如图(2),将菱形沿着AC剪开,如图(3),将△ABC经过旋转后与△ACD叠放在一起,得到四边形AA′CD,AC与A′D相交于点E,连接AA′.
(1)填空:在图(1)中,AC=
(2)请写出图(3)中三对相似三角形(不含全等三角形),并选择其中的一对加以证明;
(3)求AD:DE的值.

(1)填空:在图(1)中,AC=
4
| 3 |
4
.BD=| 3 |
4
4
.在图(3)中,四边形AA′CD是等腰
等腰
梯形;(2)请写出图(3)中三对相似三角形(不含全等三角形),并选择其中的一对加以证明;
(3)求AD:DE的值.

分析:(1)连接BD,交AC于点F,根据菱形的性质求出∠DAC的度数,利用锐角三角函数的定义可求出AF的长,故可得出AC的长,同理可求出BD的长,由图形旋转的性质可判断出四边形AA′CD的形状;
(2)根据相似三角形的判定定理可得出相似的三角形;
(3)先判断出△ADE的形状,再根据锐角三角函数的定义即可求出AD:DE的值.
(2)根据相似三角形的判定定理可得出相似的三角形;
(3)先判断出△ADE的形状,再根据锐角三角函数的定义即可求出AD:DE的值.
解答: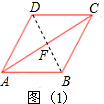 解:(1)连接BD,交AC于点F,
解:(1)连接BD,交AC于点F,
∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AF,BD=2DF,
∵AD=4,∠ADC=120°,
∴∠DAB=180°-∠ADC=180°-120°=60°,
∴∠DAC=
∠DAB=
×60°=30°,
在Rt△ADF中,AF=AD•cos30°=4×
=2
,DF=AD•sin30°=4×
=2,
∴AC=2AF=4
,BD=2DF=2×2=4,
∵AC=A′D,CD∥AA′,∠ADC=120°,
∴四边形AA′CD是等腰梯形;
故答案为:4
,4,等腰;
 (2)△CDE∽△AA′E;△ADE∽△ACA′;△A′CE∽△ADA′.
(2)△CDE∽△AA′E;△ADE∽△ACA′;△A′CE∽△ADA′.
下面证明△CDE∽△AA′E:
∵梯形ABCD是等腰梯形,AD=A′C,
∴CD∥AA′,
∴△CDE∽△AA′E;
(3)∵∠ADC=120°,∠CDE=30°,
∴∠ADE=90°,
∵∠DAE=30°,
∴
=cot30°=
.
 解:(1)连接BD,交AC于点F,
解:(1)连接BD,交AC于点F,∵四边形ABCD是菱形,
∴AC⊥BD,AC=2AF,BD=2DF,
∵AD=4,∠ADC=120°,
∴∠DAB=180°-∠ADC=180°-120°=60°,
∴∠DAC=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△ADF中,AF=AD•cos30°=4×
| ||
| 2 |
| 3 |
| 1 |
| 2 |
∴AC=2AF=4
| 3 |
∵AC=A′D,CD∥AA′,∠ADC=120°,
∴四边形AA′CD是等腰梯形;
故答案为:4
| 3 |
 (2)△CDE∽△AA′E;△ADE∽△ACA′;△A′CE∽△ADA′.
(2)△CDE∽△AA′E;△ADE∽△ACA′;△A′CE∽△ADA′.下面证明△CDE∽△AA′E:
∵梯形ABCD是等腰梯形,AD=A′C,
∴CD∥AA′,
∴△CDE∽△AA′E;
(3)∵∠ADC=120°,∠CDE=30°,
∴∠ADE=90°,
∵∠DAE=30°,
∴
| AD |
| DE |
| 3 |
点评:本题考查的是相似形综合题,此题涉及到相似三角形的判定与性质、锐角三角函数的定义,等腰梯形的判定与性质等相关知识,难度适中.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
 已知,如图四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F,垂足为O.
已知,如图四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F,垂足为O.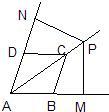 19、已知:如图,P是菱形ABCD的对角线AC延长线上一点,过P向AB、AD作垂线,垂足为M、N.求证:BM=DN.
19、已知:如图,P是菱形ABCD的对角线AC延长线上一点,过P向AB、AD作垂线,垂足为M、N.求证:BM=DN. 16、如图,AC是菱形ABCD的对角线,请你在下列条件:①分别作∠BAC、∠DAC的平分线AE、AF交BC于点E,交DC于点F;②作AE⊥BC于点E,AF⊥DC于点F.从中任选一个作为条件,证明BE=DF.
16、如图,AC是菱形ABCD的对角线,请你在下列条件:①分别作∠BAC、∠DAC的平分线AE、AF交BC于点E,交DC于点F;②作AE⊥BC于点E,AF⊥DC于点F.从中任选一个作为条件,证明BE=DF.