题目内容
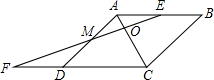 已知,如图四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F,垂足为O.
已知,如图四边形ABCD是菱形,过AB的中点E作AC的垂线EF,交AD于点M,交CD的延长线于点F,垂足为O.求证:(1)M是AD的中点;
(2)DF=
| 1 | 2 |
分析:(1)先根据EF⊥AC,可判断出EM是△ABD的中位线,继而可证得结论.
(2)由(1)得,△AME≌△DMF,则DF=AE=
CD.
(2)由(1)得,△AME≌△DMF,则DF=AE=
| 1 |
| 2 |
解答:证明:(1)连接BD,
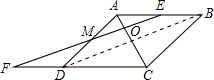
∵四边形ABCD是菱形,
∴AO平分∠BAD,AC⊥BD,
∵EF⊥AC,点E是AB中点,
∴EM是△ABD的中位线,
∴M是AD的中点;
(2)在△AME和△DMF中,
∵∠EAM=∠FDM,AM=DM,∠AME=∠DMF,
∴△AME≌△DMF,
∴DF=AE,
∵AE=
AB=
CD,
∴DF=
CD.

∵四边形ABCD是菱形,
∴AO平分∠BAD,AC⊥BD,
∵EF⊥AC,点E是AB中点,
∴EM是△ABD的中位线,
∴M是AD的中点;
(2)在△AME和△DMF中,
∵∠EAM=∠FDM,AM=DM,∠AME=∠DMF,
∴△AME≌△DMF,
∴DF=AE,
∵AE=
| 1 |
| 2 |
| 1 |
| 2 |
∴DF=
| 1 |
| 2 |
点评:本题考查了等腰三角形的判定以及全等三角形的证明,是中等题.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
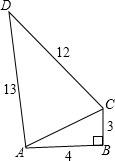 已知,如图四边形ABCD中,∠B=90°,AB=4,BC=3,AD=13,CD=12,求:四边形ABCD的面积.
已知,如图四边形ABCD中,∠B=90°,AB=4,BC=3,AD=13,CD=12,求:四边形ABCD的面积.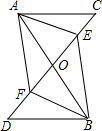 已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.
已知,如图,AB、CD相交于点O,AC∥DB,AO=BO,E、F分别是OC、OD中点.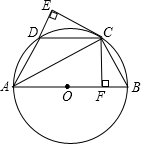 CF.
CF.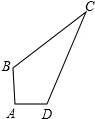 已知,如图四边形ABCD中,∠A=90°,AB=4,AD=3,CD=13,BC=12,求:四边形ABCD的面积.
已知,如图四边形ABCD中,∠A=90°,AB=4,AD=3,CD=13,BC=12,求:四边形ABCD的面积.