题目内容
(2012•邯郸二模)已知:如图1,在菱形ABCD中,E是BC的中点.过点C作CG∥EA交AD于G.
(1)求证:AE=CG;
(2)取CD的中点F,连接AF交CG于H,如图2所示.求证:AH=CH;
(3)在(2)的条件下中,若∠B=60°,直接写出△AHG与△ADF的周长比.
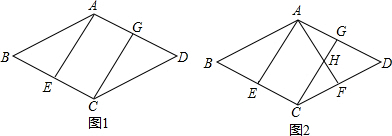
(1)求证:AE=CG;
(2)取CD的中点F,连接AF交CG于H,如图2所示.求证:AH=CH;
(3)在(2)的条件下中,若∠B=60°,直接写出△AHG与△ADF的周长比.

分析:(1)由四边形ABCD是菱形,可得CB∥DA,又由CG∥EA,即可证得四边形AECG是平行四边形,根据平行四边形的对边相等,即可证得AE=CG;
(2)由四边形AECG是平行四边形,取CD的中点F,E是BC的中点,易证得△ADF≌△CDG,然后由AAS证得△AGH≌△CFH,则可得AH=CH;
(3)首先连接AC,易得△ACD是等边三角形,则可得AF⊥CD,CG⊥AD,则可证得△AGH∽△AFD,然后由相似三角形周长的比等于相似比,求得△AHG与△ADF的周长比.
(2)由四边形AECG是平行四边形,取CD的中点F,E是BC的中点,易证得△ADF≌△CDG,然后由AAS证得△AGH≌△CFH,则可得AH=CH;
(3)首先连接AC,易得△ACD是等边三角形,则可得AF⊥CD,CG⊥AD,则可证得△AGH∽△AFD,然后由相似三角形周长的比等于相似比,求得△AHG与△ADF的周长比.
解答:(1)证明:∵四边形ABCD是菱形,
∴CB∥DA,
∵CG∥EA,
∴四边形AECG是平行四边形,
∴AE=CG;
(2)证明:由(1)可知,四边形AECG是平行四边形,
∴AG=CE,
∵四边形ABCD是菱形,
∴AD=CB=CD,
∵EC=
BC,
∴AG=GD=
CD,
∵FC=DF=
DC,
∴AG=GD=CF=DF,
在△ADF和△CDG中,
,
∴△ADF≌△CDG(SAS),
∴∠DAF=∠DCG,
在△AGH和△CFH中,
,
∴△AGH≌△CFH(AAS),
∴AH=CH;
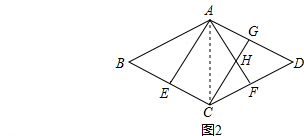 (3)解:连接AC,
(3)解:连接AC,
∵四边形ABCD是菱形,
∴∠D=∠B=60°,
∵AD=CD,
∴△ACD是等边三角形,
∵CG与AF都是△ACD的中线,
∴AF⊥CD,CG⊥AG,
∴∠AGH=∠AFD=90°,
∵∠DAF=∠HAG,
∴△AHG∽△ADF,
∵在Rt△ADF中,sin60°=
=
,
又∵AG=
AD,
∴AG:AF=
:3,
∴△AHG与△ADF的周长比为
:3.
∴CB∥DA,
∵CG∥EA,
∴四边形AECG是平行四边形,
∴AE=CG;
(2)证明:由(1)可知,四边形AECG是平行四边形,
∴AG=CE,
∵四边形ABCD是菱形,
∴AD=CB=CD,
∵EC=
| 1 |
| 2 |
∴AG=GD=
| 1 |
| 2 |
∵FC=DF=
| 1 |
| 2 |
∴AG=GD=CF=DF,
在△ADF和△CDG中,
|
∴△ADF≌△CDG(SAS),
∴∠DAF=∠DCG,
在△AGH和△CFH中,
|
∴△AGH≌△CFH(AAS),
∴AH=CH;
 (3)解:连接AC,
(3)解:连接AC,∵四边形ABCD是菱形,
∴∠D=∠B=60°,
∵AD=CD,
∴△ACD是等边三角形,
∵CG与AF都是△ACD的中线,
∴AF⊥CD,CG⊥AG,
∴∠AGH=∠AFD=90°,
∵∠DAF=∠HAG,
∴△AHG∽△ADF,
∵在Rt△ADF中,sin60°=
| AF |
| AD |
| ||
| 2 |
又∵AG=
| 1 |
| 2 |
∴AG:AF=
| 3 |
∴△AHG与△ADF的周长比为
| 3 |
点评:此题考查了菱形的性质、相似三角形的判定与性质、平行四边形的判定与性质以及全等三角形的判定与性质等知识.此题综合性较强,难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
 (2012•邯郸二模)在直角三角形ABC中,∠ACB=90°,已知AC和∠B,那么AB等于( )
(2012•邯郸二模)在直角三角形ABC中,∠ACB=90°,已知AC和∠B,那么AB等于( ) (2012•邯郸二模)如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是( )
(2012•邯郸二模)如图,在四边形ABCD中,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是( )