题目内容
【题目】如图,在△ABC和△BCD中,∠BAC=∠BCD=90°,AB=AC,CB=CD.延长CA至点E,使AE=AC;延长CB至点F,使BF=BC.连接AD,AF,DF,EF.延长DB交EF于点N.

(1)求证:AD=AF;
(2)求证:BD=EF;
(3)试判断四边形ABNE的形状,并说明理由.
【答案】(1)详见解析;(2)详见解析;(3)四边形ABNE是正方形,理由详见解析.
【解析】
试题分析:(1)根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,求得∠ABF=135°,∠ABF=∠ACD,再证得BF=CD,由SAS证明△ABF≌△ACD,即可得出AD=AF;(2)由(1)知AF=AD,△ABF≌△ACD,得出∠FAB=∠DAC,证出∠EAF=∠BAD,由SAS证明△AEF≌△ABD,得出对应边相等即可;(3)由全等三角形的性质得出得出∠AEF=∠ABD=90°,证出四边形ABNE是矩形,由AE=AB,即可得出四边形ABNE是正方形.
试题解析:(1)证明:∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∴∠ABF=135°,
∵∠BCD=90°,
∴∠ABF=∠ACD,
∵CB=CD,CB=BF,∴BF=CD,
在△ABF和△ACD中,
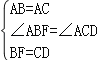 ,
,
∴△ABF≌△ACD(SAS),
∴AD=AF;
(2)证明:由(1)知,AF=AD,△ABF≌△ACD,
∴∠FAB=∠DAC,
∵∠BAC=90°,
∴∠EAB=∠BAC=90°,
∴∠EAF=∠BAD,
在△AEF和△ABD中,
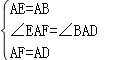 ,
,
∴△AEF≌△ABD(SAS),
∴BD=EF;
(3)解:四边形ABNE是正方形;理由如下:
∵CD=CB,∠BCD=90°,
∴∠CBD=45°,
由(2)知,∠EAB=90°,△AEF≌△ABD,
∴∠AEF=∠ABD=90°,
∴四边形ABNE是矩形,
又∵AE=AB,
∴四边形ABNE是正方形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
十进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
例如,用十六进制表示:C+F=1B,19﹣F=A,18÷4=6,则A×B=( )
A. 72 B. 6E C. 5F D. B0