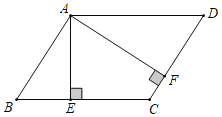
题目内容
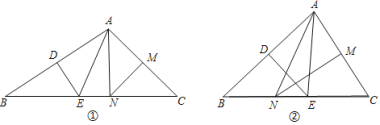
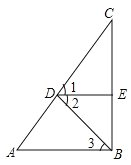
【题目】△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°.
(1)如图1,点E在BC上,则线段AE和BD有怎样的关系?请直接写出结论(不需证明);
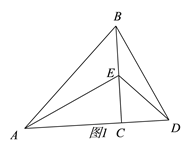
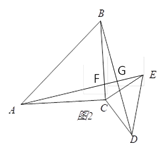
(2)若将△DCE绕点C旋转一定的角度得图2,则(1)中的结论是否仍然成立?请说明理由;
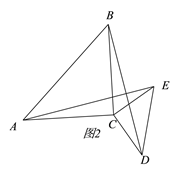
(3)当△DCE旋转到使∠ADC=90°时,若AC=5,CD=3,求BE的长.
【答案】(1)AE=BD,AE⊥BD ;(2)见解析;(3)![]()
【解析】分析:(1)延长AE交BD于F,由△AEC≌△BDC,可得AE=BD,再利用同角的余角相等,可得出AE⊥BD ;(2)不发生变化,只要证明△AEC≌△BDC,推出AE=BD,∠EAC=∠DBC,由∠EAC+∠AFC =90°,∠AFC=∠BFG,可得∠BGF=90°,从而得证;(3)过B作BM⊥EC于M,则∠M=90°,在RT△ACD中利用勾股定理可得AD=4,再利用△BCM≌△ACD,得出CM=CD=3, BM=AD=4,在△BME中利用勾股定理即可求出结果.
本题解析:
(1)AE=BD,AE⊥BD ;
(2)(1)中的结论仍然成立,理由如下:
∵△ACB和△ECD均为等腰直角三角形,∠ACB=∠ECD=90°
∴AC=BC, ∠ACE=∠BCD,EC=DC
∴△ACE≌△BCD(SAS), ∴AE=BD, ∠EAC=∠DBC
∵∠EAC+∠AFC =90°,∠AFC=∠BFG
∴∠DBC+∠BFG=90°, ∴∠BGF=90°,
∴AE⊥BD
(3) 过B作BM⊥EC于M,则∠M=90°
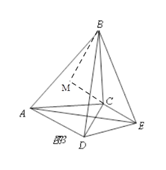
∵∠ADC=90°,AC=5,CD=3,∴AD=![]()
∵∠ACB=∠ECD=90°, ∴∠CBE+∠ACD=180°
∵∠CBE+∠BCM=180°, ∴∠BCM=∠ACD
∵∠M=∠ADC=90°, AC=BC
∴△BCM≌△ACD(AAS), ∴CM=CD=3, BM=AD=4
∵CE=CD=3,∴EM=6,
∴BE=![]()

【题目】现有一个种植总面积为![]() 的矩形塑料温棚,分垄间隔套种草莓和西红柿共
的矩形塑料温棚,分垄间隔套种草莓和西红柿共![]() 垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过
垄,种植的草莓或西红柿单种农作物的总垄数不低于8垄,又不超过![]() 垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
垄(垄数为正整数),它们的占地面积、产量、利润分别如下:
⑴若设草莓共种植了![]() 垄,通过计算说明共有几种种植方案?分别是哪几种?
垄,通过计算说明共有几种种植方案?分别是哪几种?
⑵在这几种种植方案中,哪种方案获得的利润最大?最大利润是多少?
占地面积(m2/垄) | 产量(千克/垄) | 利润(元/千克) | |
西红柿 | 32 | 160 | 1.0 |
草莓 | 15 | 50 | 1.6 |