题目内容
【题目】在黄冈长江大桥的东端一处空地上,有一块矩形的标语牌ABCD(如图所示),已知标语牌的高AB=5m,在地面的点E处,测得标语牌点A的仰角为30°,在地面的点F处,测得标语牌点A的仰角为75°,且点E,F,B,C在同一直线上,求点E与点F之间的距离.(计算结果精确到0.1米,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)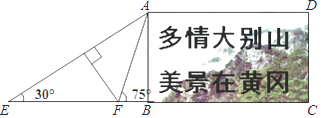
【答案】解:如图作FH⊥AE于H.
由题意可知∠HAF=∠HFA=45°,
∴AH=HF,设AH=HF=x,则EF=2x,EH= ![]() x,
x,
在Rt△AEB中,∵∠E=30°,AB=5米,
∴AE=2AB=10米,
∴x+ ![]() x=10,
x=10,
∴x=5 ![]() ﹣5,
﹣5,
∴EF=2x=10 ![]() ﹣10≈7.3米,
﹣10≈7.3米,
答:E与点F之间的距离为7.3米.
【解析】根据勾股定理得到各个边的关系,再根据在直角三角形中,30度角所对的边是斜边的一半,求出点E与点F之间的距离.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目