题目内容
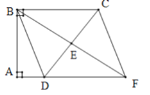
【题目】已知:PA、PB、EF分别切⊙O于A、B、D,若PA=15cm,那么△PEF周长是cm.若∠P=50°,那么∠EOF= . 
【答案】30;65°
【解析】解:∵PA、PB、EF分别切⊙O于A、B、D,
∴PA=PB=15cm,ED=EA,FD=DB,
∴PE+EF+PF=PE+ED+PF+FD=PA+PB=30(cm)即△PEF周长是30cm;
∵PA、PB为⊙O的切线,
∴∠PAO=∠PBO=90°,
而∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°;
连OD,如图,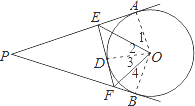
∴∠ODE=∠ODF=90°,
易证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,
∴∠1=∠2,∠3=∠4,
∴∠2+∠3= ![]() ∠AOB=65°,则∠EOF=65°.
∠AOB=65°,则∠EOF=65°.
根据切线长定理证得ED=EA,FD=DB,再根据△PEF周长=PE+EF+PF,证得△PEF周长等于2PA。即可得出答案;连接OD,OA,OB。根据直角三角形的全等判定证得Rt△OAE≌Rt△ODE,Rt△OFD≌Rt△OFB,再根据全等三角形的性质得出∠1=∠2,∠3=∠4,就可证得∠EOF=![]() ∠AOB。再在四边形APBO中根据四边形的内角和定理求出∠AOB的度数,即可求出∠EOF的度数。
∠AOB。再在四边形APBO中根据四边形的内角和定理求出∠AOB的度数,即可求出∠EOF的度数。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目