题目内容
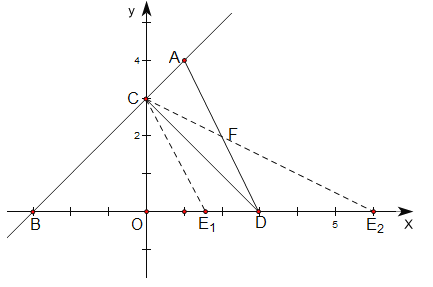
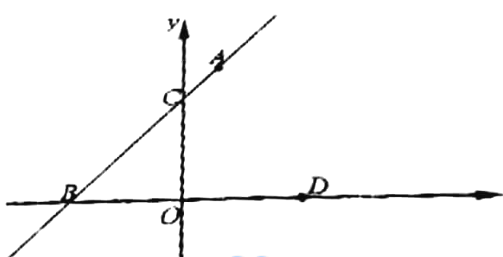
【题目】如图，已知一次函数y=kx+3的图形经过点A (1， m)，与x轴、y轴分别相交于B、C两点，且∠ABO=45°，设点D的坐标为(3，0)
(1) 求m的值；
(2) 联结CD、AD，求△ACD的面积；
(3) 设点E为x轴上一动点，当∠ADC=∠ECD时，求点E的坐标．
【答案】（1）m＝4；（2）
；（3）点E的坐标为（
，0）或（6，0）．
【解析】
（1）求出点B坐标，利用待定系数法求出直线BC的解析式即可解决问题；
（2）根据
进行计算即可；
（3）分点E在点D左侧和点E在点D右侧两种情况，分别求出直线CE1和直线CE2的解析式即可得到对应的点E的坐标．
解：（1）∵一次函数y=kx+3的图象与x轴、y轴分别相交于B、C两点，∠ABO=45°，
∴OB＝OC＝3，
∴B（－3，0），
将B（－3，0）代入y=kx+3得：0=－3k+3，
解得：k＝1，
∴直线BC的解析式为：y＝x+3，
当x＝1时，y＝x+3＝4，
∴m＝4；
（2）∵B（－3，0），C（0，3），D（3，0），A（1，4），
∴BD＝6，
∴
；
（3）如图所示，当点E在点D左侧时，
∵∠ADC＝∠E1CD，
∴AD∥CE1，
设直线AD的解析式为：y＝k1x+b（k≠0），
代入A（1，4），D（3，0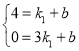）得：
，解得：
，
∴直线AD的解析式为：
，
故设直线CE1的解析式为：
，
代入C（0，3）得：
，
∴直线CE1的解析式为：
，
当y＝0时，解得：
，
∴E1（，0）；
当点E在点D右侧时，AD与CE2交于点F，
∵∠ADC＝∠E2CD，
∴FC＝FD，
∵OB＝OD＝3，∠ABO＝45°，
∴∠CDB＝45°，
∴∠ACD＝45°＋45°＝90°，即∠ACF＋∠FCD＝90°，
∵∠CAF＋∠FDC＝90°，
∴∠ACF＝∠CAF，
∴FC＝FA，
∴F为线段AD的中点，
∴点F的坐标为
，
设直线CE2的解析式为：
，
代入F得：
，解得：
，
∴直线CE2的解析式为：
，
当y＝0时，解得：
，
∴E2（6，0），
综上所述，点E的坐标为（，0）或（6，0）．
