Question

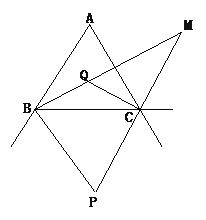
【题目】已知：如图所示，在△ABC中，∠BAC=60°，AD=AE，BE、CD交于点F，且∠DFE=120°.在BE的延长线上截取ET=DC，连接AT.

（1）求证：∠ADC=∠AET；

（2）求证：AT=AC；

（3）设BC边上的中线AP与BE交于Q.求证：∠QAB=∠QBA.

Answer 1

【答案】（1）见解析 （2）见解析 （3）见解析

【解析】

（1）根据已知条件求得∠AEF+∠ADC=180°，再根据∠AEF+∠AET=180°即可得∠ADC=∠AET；

（2）利用SAS可证△AET≌△ADC即可解答；

（3）延长AP至G点，使得GP=AP，连接BG.，再利用SAS可证△APC≌△GPB的性质证明出△ABG≌△BAT即可解答.

（1）∵∠BAC=60°，∠DFE=120°，

∴∠AEF+∠ADC=360°-60°-120°=180°.

∵∠AEF+∠AET=180°

∴∠ADC=∠AET.

（2）利用SAS可证△AET≌△ADC.

∴AT=AC.

（3）延长AP至G点，使得GP=AP，连接BG.

利用SAS可证△APC≌△GPB.

∴AC=GB

由（2）可知AC=AT

∴GB=AT

由（2）可知∠TAC=∠CAD=60°

∴∠TAB=120°

又∵△APC≌△GPB，∴∠CAP=∠BGP，∴AC∥BG

∴∠ABG=180°-∠BAC=180°-60°=120°=∠TAB

利用SAS可证△ABG≌△BAT，

∴∠QAB=∠QBA.