题目内容
【题目】如图,边长为1的菱形ABCD中,∠DAB=60°.连结对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°.连结AE,再以AE为边作第三个菱形AEGH使∠HAE=60°…按此规律所作的第n个菱形的边长是 . 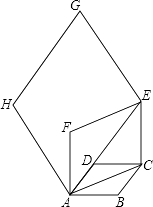
【答案】( ![]() )n﹣1
)n﹣1
【解析】解:连接DB,
∵四边形ABCD是菱形,
∴AD=AB.AC⊥DB,
∵∠DAB=60°,
∴△ADB是等边三角形,
∴DB=AD=1,
∴BM= ![]() ,
,
∴AM= ![]() ,
,
∴AC= ![]() ,
,
同理可得AE= ![]() AC=(
AC=( ![]() )2 , AG=
)2 , AG= ![]() AE=3
AE=3 ![]() =(
=( ![]() )3 ,
)3 ,
按此规律所作的第n个菱形的边长为( ![]() )n﹣1 ,
)n﹣1 ,
故答案为( ![]() )n﹣1 .
)n﹣1 . 
连接DB于AC相交于M,根据已知和菱形的性质可分别求得AC,AE,AG的长,从而可发现规律根据规律不难求得第n个菱形的边长.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
