题目内容
【题目】如图，小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°，然后前进12米到达C处，又测得楼顶E的仰角为60°，求楼EF的高度．（结果保留根号）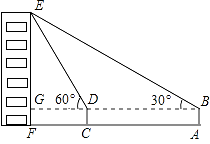
【答案】解：设楼EF的高为x米，可得EG=EF﹣GF=（x﹣1.5）米，
依题意得：EF⊥AF，DC⊥AF，BA⊥AF，BD⊥EF（设垂足为G），
在Rt△EGD中，DG= 
= 
（x﹣1.5）米，在Rt△EGB中，BG= 
（x﹣1.5）米，
∴CA=DB=BG﹣DG= 
（x﹣1.5）米，
∵CA=12米，∴ （x﹣1.5）=12，
解得：x=6 +1.5
则楼EF的高度为6 +1.5米．
【解析】求EF，而EF=EG+GF，GF=AB=1.5米，则EG=EF-1.5，在Rt△EGD中，根据60度，可知EG和GD的数量关系，则可用EF来表示DG；在Rt△BEG中,由30度角，可以用EF表示出BG，从而根据BG-GD=12米，构造方程，解出EF.
【考点精析】根据题目的已知条件，利用关于仰角俯角问题的相关知识可以得到问题的答案，需要掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
练习册系列答案
相关题目
