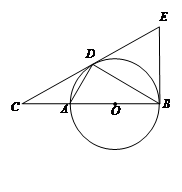题目内容
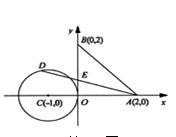
如图,已知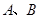 两点的坐标分别为
两点的坐标分别为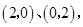
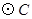 的圆心坐标为
的圆心坐标为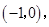 半径为1.若
半径为1.若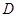 是
是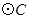 上的一个动点,线段
上的一个动点,线段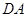 与
与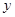 轴交于点
轴交于点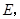 则
则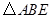 面积的最小值是( )
面积的最小值是( )
 两点的坐标分别为
两点的坐标分别为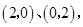
 的圆心坐标为
的圆心坐标为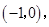 半径为1.若
半径为1.若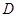 是
是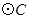 上的一个动点,线段
上的一个动点,线段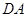 与
与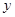 轴交于点
轴交于点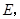 则
则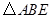 面积的最小值是( )
面积的最小值是( )
A.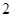 | B.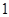 | C.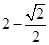 | D.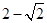 |
C
若△ABE的面积最小,则AD与⊙C相切,连接CD,则CD⊥AD;
Rt△ACD中,CD=1,AC=OC+OA=3;由勾股定理,得:AD=2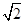 ;∴S△ACD=
;∴S△ACD=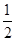 AD•CD=
AD•CD=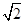 ;
;
易证得△AOE∽△ADC,∴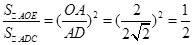 ,即S△AOE=
,即S△AOE=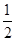 S△ADC=
S△ADC=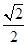 ;
;
∴S△ABE=S△AOB-S△AOE=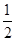 ×2×2-
×2×2-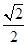 =2-
=2-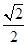 ;故选C.
;故选C.
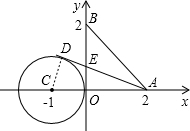
Rt△ACD中,CD=1,AC=OC+OA=3;由勾股定理,得:AD=2
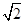 ;∴S△ACD=
;∴S△ACD=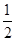 AD•CD=
AD•CD=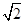 ;
;易证得△AOE∽△ADC,∴
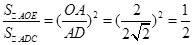 ,即S△AOE=
,即S△AOE=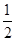 S△ADC=
S△ADC=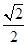 ;
;∴S△ABE=S△AOB-S△AOE=
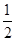 ×2×2-
×2×2-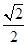 =2-
=2-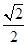 ;故选C.
;故选C.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
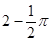
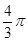

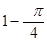

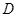 为
为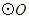 上一点,点
上一点,点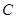 在直径
在直径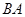 的延长线上,
的延长线上,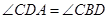 .
.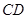 是
是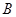 作
作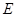 ,若
,若 ,求
,求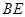 的长.
的长.