题目内容
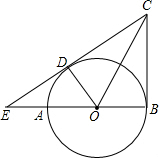 如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,CE与BA的延长线交于点E,连接OC、OD.
如图,AB是⊙O的直径,CB、CE分别切⊙O于点B、D,CE与BA的延长线交于点E,连接OC、OD.(1)△OBC与△ODC是否全等?
(2)已知DE=a,AE=b,BC=c,请你思考后,选用以上适当的数,设计出计算⊙O半径r的一种方案:
①你选用的已知数是
②写出求解过程.(结果用字母表示)
分析:(1)由切线和切线长定理可知,∠ODC=∠OBC=90°,OD=OB,OC=OC从而得到△OBC≌△ODC(HL);
(2)可选择a,b,c或其中的两个.求由勾股定理求解或切割线定理求解.
(2)可选择a,b,c或其中的两个.求由勾股定理求解或切割线定理求解.
解答:解:(1)△OBC与△ODC全等.
证明:∵CD、CB是⊙O的切线
∴∠ODC=∠OBC=90°
∵OD=OB,OC=OC
∴△OBC≌△ODC(HL);
(2)①选择a、b、c,或其中2个;
②若选择a、b:由切割线定理:a2=b(b+2r),得r=
若选择a、b、c:
方法一:在Rt△EBC中,由勾股定理:(b+2r)2+c2=(a+c)2,得r=
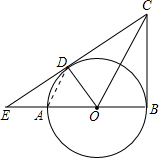
方法二:Rt△ODE∽Rt△CBE,
=
,得r=
方法三:连接AD,可证:AD∥OC,
=
,得r=
若选择a、c:需综合运用以上的多种方法,得r=
若选择b、c,则有关系式2r3+br2-bc2=0.
证明:∵CD、CB是⊙O的切线
∴∠ODC=∠OBC=90°
∵OD=OB,OC=OC
∴△OBC≌△ODC(HL);
(2)①选择a、b、c,或其中2个;
②若选择a、b:由切割线定理:a2=b(b+2r),得r=
| a2-b2 |
| 2b |
若选择a、b、c:
方法一:在Rt△EBC中,由勾股定理:(b+2r)2+c2=(a+c)2,得r=
| ||
| 2 |

方法二:Rt△ODE∽Rt△CBE,
| a |
| r |
| b+2r |
| c |
-b+
| ||
| 4 |
方法三:连接AD,可证:AD∥OC,
| a |
| c |
| b |
| r |
| bc |
| a |
若选择a、c:需综合运用以上的多种方法,得r=
c
| ||
| a+2c |
若选择b、c,则有关系式2r3+br2-bc2=0.
点评:本题考查了切线的概念,切线长定理,勾股定理及全等三角形的判定等知识点的综合运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( )
8、如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为( ) 0.1平方米)
0.1平方米)

 如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为
如图,AB是铅直地竖立在坡角为30°的山坡上的电线杆,当阳光与水平线成60°角时,电线杆的影子BC的长度为4米,则电线杆AB的高度为