题目内容
如图1,在?ABCD中,AD=a,AB=
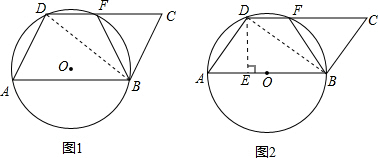
a,a为定值,线段AD绕着点A旋转,旋转时∠DAB为锐角,经过A、D、B三点的圆⊙O和边CD相交于点F,点F不与点D重合.
(1)求∠DAB的范围;
(2)如果AD旋转到使得AB刚好成为⊙O的直径(如图2所示),请你验证此时∠DAB的度数在第(1)问所求的范围内,并证明:此时点F恰好是DC的一个三等分点.

| 3 |
(1)求∠DAB的范围;
(2)如果AD旋转到使得AB刚好成为⊙O的直径(如图2所示),请你验证此时∠DAB的度数在第(1)问所求的范围内,并证明:此时点F恰好是DC的一个三等分点.

分析:(1)连接DB,当F与D重合时,即CD与圆相切,根据平行四边形的性质推出∠DAB=∠DBA,求出等腰三角形DAB,求出∠DAB的度数即可;
(2)求出cos∠DAB的值,即可推出∠DAB的大小;根据CD和CF的长,根据DF=CD-CF,代入求出即可.
(2)求出cos∠DAB的值,即可推出∠DAB的大小;根据CD和CF的长,根据DF=CD-CF,代入求出即可.
解答:(1)解:连接DB,
当F与D重合时,此时CD与圆相切.
∴∠CDB=∠DAB,
∵平行四边形ABCD,
∴CD∥AB,
∴∠CDB=∠DBA,
∴∠DAB=∠DBA,
∴△ADB是等腰三角形,底为根号
a,腰为a
∴cos∠DAB=
=
,
∴∠DAB=30°,
即∠DAB的范围为:30°<∠DAB<90°.
(2)解:∵AB为⊙O的直径,
∴⊙O的半径r=
AB=
a
∵∠ADB=90°,
∴cos∠DAB=
=
=
<
,
∴∠DAB在30°<∠DAB<90°的范围内.
∵DF=AB=2AE=AB-2ADcos∠DAB=
a-2a×
=
a=
AB=
CD,
∴此时点F恰好是DC的一个三等份点.
当F与D重合时,此时CD与圆相切.
∴∠CDB=∠DAB,
∵平行四边形ABCD,
∴CD∥AB,
∴∠CDB=∠DBA,
∴∠DAB=∠DBA,
∴△ADB是等腰三角形,底为根号
| 3 |
∴cos∠DAB=
| ||||
| a |
| ||
| 2 |
∴∠DAB=30°,
即∠DAB的范围为:30°<∠DAB<90°.
(2)解:∵AB为⊙O的直径,
∴⊙O的半径r=
| 1 |
| 2 |
| ||
| 2 |
∵∠ADB=90°,
∴cos∠DAB=
| AD |
| AB |
| 1 | ||
|
| ||
| 3 |
| ||
| 2 |

∴∠DAB在30°<∠DAB<90°的范围内.
∵DF=AB=2AE=AB-2ADcos∠DAB=
| 3 |
| ||
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴此时点F恰好是DC的一个三等份点.
点评:本题综合考查了平行四边形的性质,等腰三角形的性质和判定,勾股定理,圆心角、弧、弦之间的关系,平行线的性质等知识点,此题综合性比较强,对学生有较高的要求.

练习册系列答案
相关题目
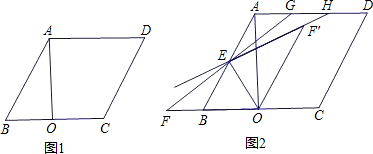
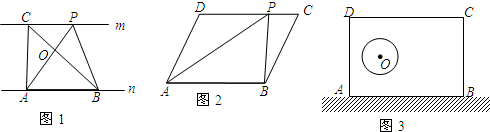



 )时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.
)时,作EF⊥DP于点F,连接AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论.