题目内容
【题目】如图,直线AB∥CD,∠FGH=90°,∠GHM= 40°,∠HMN=30°,并且∠EFA的两倍比∠CNP大10°,则∠PND的大小是( )

A. 100°B. 120°C. 130°D. 150°
【答案】C
【解析】
作辅助线:延长PM、EG交于点K;EG的延长线交CD于点O,PM延长线交AB于点L,利用平行线性质进行求解.
延长PM、EG交于点K;EG的延长线交CD于点O,PM延长线交AB于点L,如图,
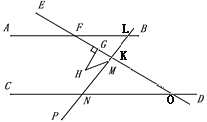
∵∠HMN=30゜,
∴∠HMK=150゜,
在四边形GHMK中,∠HGK=90゜,∠GHM=40゜,∠HMK=150゜,
∴∠GKM=360゜-∠HGK-∠GHM-∠HMK=360゜-90゜-40゜-150゜=80゜,
∴∠FKL=100゜,
∴∠NKO=100゜,
设∠EFA =x,则∠PNC =2x-10゜,
∴∠KNO=2x-10゜,
∵AB∥CD,
∴∠KON=∠EFA=x,
∵∠KNO+∠NKO+∠KON=180゜,
∴2x-10゜+x+100゜=180゜,解得,x=30゜,
∴∠PNC=2×30゜-10゜=50゜,
∴∠PND=180゜-50゜=130゜.
故选C.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】某饮料厂开发了A、B两种新型饮料,主要原料均为甲和乙,每瓶饮料中甲、乙的含量如下表所示.现用甲原料和乙原料各2800克进行试生产,计划生产A、B两种饮料共100瓶.设生产A种饮料x瓶,解析下列问题:
原料名称 饮料名称 | 甲 | 乙 |
A | 20克 | 40克 |
B | 30克 | 20克 |
(1)有几种符合题意的生产方案写出解析过程;
(2)如果A种饮料每瓶的成本为2.60元,B种饮料每瓶的成本为2.80元,这两种饮料成本总额为y元,请写出y与x之间的关系式,并说明x取何值会使成本总额最低?