题目内容
【题目】如图,已知四边形ABCD,AD∥BC.点P在直线CD上运动(点P和点C,D不重合,点P,A,B不在同一条直线上),若记∠DAP,∠APB,∠PBC分别为∠α,∠β,∠γ.
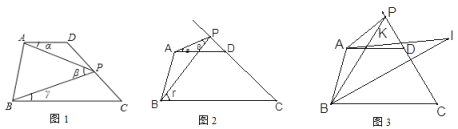
(1)如图1,当点P在线段CD上运动时,写出∠α,∠β,∠γ之间的关系并说出理由;
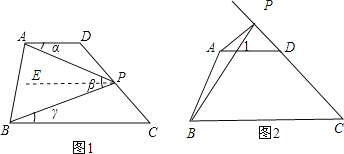
(2)如图2,如果点P在线段CD的延长线上运动,探究∠α,∠β,∠γ之间的关系,并说明理由.
(3)如图3,BI平分∠PBC,AI交BI于点I,交BP于点K,且∠PAI:∠DAI=5:1,∠APB=20°,∠I=30°,求∠PAI的度数.
【答案】(1)∠β=∠α+∠γ. 理由见解析;(2)点P在线段CD的延长线上运动时,∠β=∠γ﹣∠α;点P在线段DC的延长线上运动时,∠β=∠α﹣∠γ;理由见解析;(3)∠PAI=50°.
【解析】
(1)过点P作PE∥AD,如图1,由PE∥AD得∠α=∠APE,由AD∥BC得PE∥BC,则∠γ=∠BPE,所以∠β=∠APE+∠BPE=∠α+∠γ;
(2)点P在线段CD的延长线上运动时,∠β=∠γ-∠α;点P在线段DC的延长线上运动时,∠β=∠α-∠γ.以点P在线段CD的延长线上运动为例说明:
如图2,根据平行线的性质由AD∥BC得∠PBC=∠1,根据三角形外角性质得∠1=∠PAD+∠APB,所以∠APB=∠PBC-∠PAD,即∠β=∠γ-∠α.
(3)根据题意可设∠PBI=∠CBI=m,则∠CBP=2m,∠PAI=m+10°,由∠PAI:∠DAI =5:1得∠DAI=![]() m+2°,根据∠DHP是△APH的外角列出方程求解即可.
m+2°,根据∠DHP是△APH的外角列出方程求解即可.
(1)∠β=∠α+∠γ.
理由如下:
过点P作PE∥AD,如图1,
∵PE∥AD,
∴∠α=∠APE,
∵AD∥BC,
∴PE∥BC,
∴∠γ=∠BPE,
∴∠β=∠APE+∠BPE=∠α+∠γ;
(2)点P在线段CD的延长线上运动时,∠β=∠γ﹣∠α;点P在线段DC的延长线上运动时,∠β=∠α﹣∠γ.
以点P在线段CD的延长线上运动为例说明:
如图2,
∵AD∥BC,
∴∠PBC=∠1,
而∠1=∠PAD+∠APB,
∴∠APB=∠PBC﹣∠PAD,
即∠β=∠γ﹣∠α.
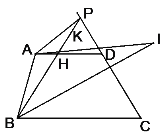
(3)∵BI平分∠ABC,
∴可设∠PBI=∠CBI=m,则∠CBP=2m,
∵AD∥BC,
∴∠DHP=∠CBP=2m,
∵∠APB=20°,∠I=30°,∠BKI=∠AKP,
∴∠PAI=m+30°﹣20°=m+10°,
又∵∠PAI:∠DAI =5:1,
∴∠DAI=![]() ∠PAI=
∠PAI=![]() m+2°,
m+2°,
∵∠DHP是△APH的外角,
∴∠DHP=∠PAH+∠APB,
即2m=![]() m+2°+m+10°+20°,
m+2°+m+10°+20°,
解得m=40°,
∴∠PAI=40°+10°=50°.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案【题目】某篮球队对队员进行定点投篮测试,每人每天投篮10次,现对甲、乙两名队员在五天中进球数(单位:个)进行统计,结果如下:
甲 | 10 | 6 | 10 | 6 | 8 |
乙 | 7 | 9 | 7 | 8 | 9 |
经过计算,甲进球的平均数为8,方差为3.2.
(1)求乙进球的平均数和方差;
(2)如果综合考虑平均成绩和成绩稳定性两方面的因素,从甲、乙两名队员中选出一人去参加定点投篮比赛,应选谁?为什么?
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
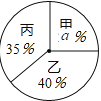
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.





