Question

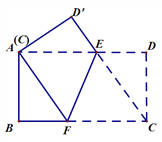
【题目】如图，将矩形ABCD折叠，使C点与A点重合，折痕为EF.

（1）判断四边形AFCE的形状，并说明理由；

（2）若AB=4，BC=8，求折痕EF的长.

Answer 1

【答案】（1）四边形AFCE是菱形，理由见解析；

（2）折痕EF的长是

【解析】解：（1）四边形AFCE是菱形．

理由如下：

由题意可知，AF=CF，AE=CE，

且∠AFE=∠CFE，

∵矩形ABCD，∴AD∥BC，

∴∠AEF=∠CFE，

∴∠AEF=∠AFE，

∴AE=AF=CF=CE

∴四边形AFCE是菱形；

设BF=x，则AF=CF=8-x，

在△ABF中，由勾股定理得，AB2+BF2=AF2，

即42+x2=（8-x）2，

解得，x=3，∴AF=5，

∴，

∵四边形AFCE是菱形，

∴AC⊥EF，由，得EF=

此题解法不唯一，请酌情评分．