题目内容
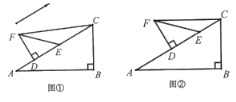
【题目】已知:如图,在等边![]() 中,
中,![]() ,且
,且![]() 交
交![]() 外角平分线
外角平分线![]() 于点
于点![]() .
.

(1)当点![]() 为
为![]() 中点时,试说明
中点时,试说明![]() 与
与![]() 的数量关系;
的数量关系;
(2)当点![]() 不是
不是![]() 中点时,试说明
中点时,试说明![]() 与
与![]() 的数量关系.
的数量关系.
【答案】(1)![]() ,见解析.(2)
,见解析.(2)![]() ,见解析.
,见解析.
【解析】
(1)AD=DE.由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(2)AD=DE.由等边三角形的性质和平行线的性质得到∠BDF=∠BFD=60°,于是得到△BDF是等边三角形,再证明△AFD≌△DCE即可得到结论;
(1)结论:AD=DE,理由如下:
如图: 过点D作DF∥AC,交AB于点F,
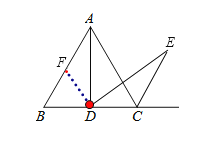
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°.
又∵DF∥AC,
∴∠BDF=∠ACB=60°,
∴△BDF是等边三角形,
∴DF=BD,∠BFD=60°,
∵BD=CD,
∴DF=CD
∴∠AFD=120°.
∵EC是外角的平分线,∴∠ACE=60°,
∴∠DCE=∠ACB+∠ACE=120°=∠AFD,
∵∠ADB=∠ADC=90°,
∴∠ADF=∠EDC=30°,
在△AFD与△EDC中,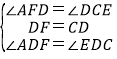 ,
,
∴△AFD≌△DCE(ASA),
∴AD=DE;
(2)结论:AD=DE;理由如下:
如图2,过点D作DF∥AC,交AB于点F,
∵△ABC是等边三角形,
∴AB=BC,∠B=∠ACB=∠ABC=60°,
又∵DF∥AC,
∴∠BDF=∠ACB=60°,
∴△BDF是等边三角形,∴BF=BD,∠BFD=60°,
∴AF=CD,∠AFD=120°,
∵EC是外角的平分线,∴∠ACE=60°,
∴∠DCE=∠ACB+∠ACE=120°=∠AFD,
∵∠ADC是△ABD的外角,
∴∠ADC=∠B+∠FAD=60°+∠FAD,
∵∠ADC=∠ADE+∠EDC=60°+∠EDC,
∴∠FAD=∠EDC,
在△AFD和△DCE中,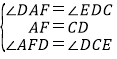 ,
,
∴△AFD≌△DCE(ASA),
∴AD=DE.