题目内容
记Sn=a1+a2+…+an,令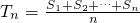 ,称Tn为a1,a2,…,an这列数的“理想数”.已知a1,a2,…,a500的“理想数”为2004,那么8,a1,a2,…,a500的“理想数”为
,称Tn为a1,a2,…,an这列数的“理想数”.已知a1,a2,…,a500的“理想数”为2004,那么8,a1,a2,…,a500的“理想数”为
- A.2004
- B.2006
- C.2008
- D.2010
C
分析:本题需先根据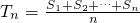 得出n×Tn=(S1+S2+…+Sn),再根据a1,a2,…,a500的“理想数”为2004,得出T500的值,再设出新的理想数为Tx
得出n×Tn=(S1+S2+…+Sn),再根据a1,a2,…,a500的“理想数”为2004,得出T500的值,再设出新的理想数为Tx
,列出式子,把得数代入,即可求出结果.
解答:∵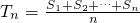
∴n×Tn=(S1+S2+…+Sn)
T500=2004
设新的理想数为Tx
501×Tx=8×501+500×T500
Tx=(8×501+500×T500)÷501
=
=8+500×4
=2008
故选C
点评:本题主要考查了有理数的混合运算,在解题时要根据题意找出关系是解题的关键.
分析:本题需先根据
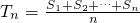 得出n×Tn=(S1+S2+…+Sn),再根据a1,a2,…,a500的“理想数”为2004,得出T500的值,再设出新的理想数为Tx
得出n×Tn=(S1+S2+…+Sn),再根据a1,a2,…,a500的“理想数”为2004,得出T500的值,再设出新的理想数为Tx,列出式子,把得数代入,即可求出结果.
解答:∵
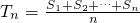
∴n×Tn=(S1+S2+…+Sn)
T500=2004
设新的理想数为Tx
501×Tx=8×501+500×T500
Tx=(8×501+500×T500)÷501
=

=8+500×4
=2008
故选C
点评:本题主要考查了有理数的混合运算,在解题时要根据题意找出关系是解题的关键.

练习册系列答案
相关题目
 ,称Tn为a1,a2,…,an这列数的“理想数”.已知a1,a2,…,a500的“理想数”为2004,那么8,a1,a2,…,a500的“理想数”为( )
,称Tn为a1,a2,…,an这列数的“理想数”.已知a1,a2,…,a500的“理想数”为2004,那么8,a1,a2,…,a500的“理想数”为( ) ,称Tn为a1,a2,…,an这列数的“理想数”.已知a1,a2,…,a500的“理想数”为2004,那么8,a1,a2,…,a500的“理想数”为( )
,称Tn为a1,a2,…,an这列数的“理想数”.已知a1,a2,…,a500的“理想数”为2004,那么8,a1,a2,…,a500的“理想数”为( )