题目内容
【题目】在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a (a<0)经过点A(-1,0),将点B(0,4)向右平移5个单位长度,得到点C.
(1)求点C的坐标;
(2)求抛物线的对称轴;
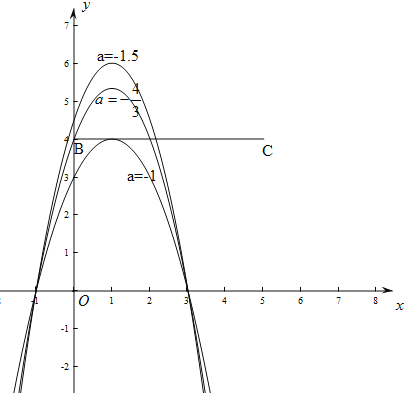
(3)若抛物线与线段BC恰有一个公共点,结合函数图像,求a的取值范围.
【答案】(1)C(5,4);(2)x=1; (3) ![]() 或
或![]()
【解析】
(1)根据坐标平移的特点是左减右加、上加下减可以求得点C的坐标;
(2)根据抛物线C1:y=ax2﹣2ax﹣3a(a≠0)可以求得该抛物线的对称轴;
(3)分三种情况讨论:①当抛物线顶点在线段BC上时,②当抛物线与直线BC的左交点在B的左边,右交点在线段BC上时,③当抛物线与直线BC的左交点在线段BC上,右交点在线段BC的延长线上时.
(1)∵点B(0,4)向右平移5个单位长度,得到点C,
∴点C的坐标为(5,4);
(2)∵抛物线C1:y=ax2﹣2ax﹣3a,
∴对称轴是直线x=﹣![]() =1;
=1;
(3)∵y=ax2﹣2ax﹣3a=a(x-1)2﹣4a,
∴分三种情况讨论:
①当抛物线顶点在线段BC上时,抛物线与线段BC只有一个交点,此时﹣4a=4,
解得:a=-1;
②当抛物线与直线BC的左交点在B的左边,右交点在线段BC上时,抛物线与线段BC只有一个交点,此时抛物线与y轴的交点在点B上方,
∴-3a>4,
解得:a<![]() .
.
③当抛物线与直线BC的左交点在线段BC上,右交点在线段BC的延长线上时,抛物线与线段BC只有一个交点.
∵抛物线开口向下,此时抛物线与x轴的右交点的横坐标一定大于5,这与抛物线一定过(-1,0)和(3,0)矛盾,此种情况不成立.
综上所述:a的取值范围是![]() 或a=-1.
或a=-1.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目