Question

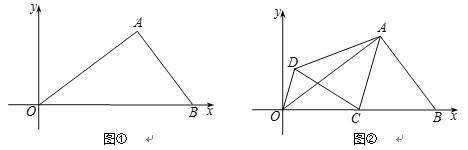
【题目】把三角形纸片放置在平面直角坐标系中，点(，)，点在轴的正半轴上，且．

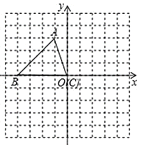
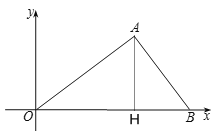
（1）如图①，求，的长及点的坐标；

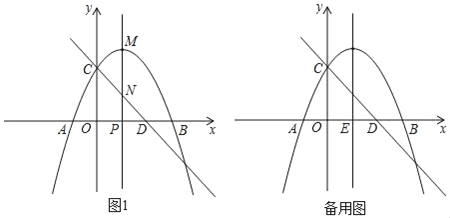
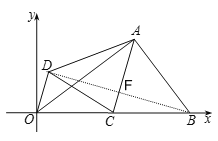
（2）如图②，点是的中点，将△沿翻折得到△，

①求四边形的面积；

②求证：△是等腰三角形；

③求的长（直接写出结果即可）．

Answer 1

【答案】（1）OA＝4，AB＝3，B（5，0）；（2）①四边形的面积为6；②见解析；③OD＝．

【解析】

（1）过A作AH⊥OB于H，根据A点坐标及求出OH、AH和HB的长，利用勾股定理可得，的长，同时可得点的坐标；

（2）①求出的面积，即可得到四边形的面积；

②根据勾股定理逆定理可得是直角三角形，根据直角三角形斜边中线的性质求出AC＝BC即可得证；

③连接BD交AC于F，证明OD∥AC，可得CF是△OBD的中位线，设CF＝x，则AF＝，根据勾股定理构建方程求出x即可解决问题．

解：（1）如图，过A作AH⊥OB于H，

∵(，)，，

∴OH＝，AH＝，HB＝5－，

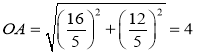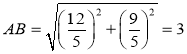∴，，B点坐标为（5，0）；

（2）①由（1）可知△ABC的边BC上的高为，BC＝，

∴，

∵将沿翻折得到，

∴四边形的面积＝2；

②∵OA＝4，AB＝3，OB＝5，

∴AB2＋OA2＝OB2，

∴是直角三角形，

∵点是的中点，

∴AC＝BC＝OC，即是等腰三角形；

③连接BD交AC于F，

由折叠的性质可得：BD⊥AC，CB＝CD＝，AD＝AB＝3，∠ACD＝∠ACB，

∴AC＝BC＝OC＝CD＝，

∴∠COD＝∠CDO，

∵∠COD＋∠CDO＋∠OCD＝180°，∠ACD＋∠ACB＋∠OCD＝180°，

∴∠ACB＝∠COD，

∴OD∥AC，

∵点是的中点，

∴CF是△OBD的中位线，即OD＝2CF，

设CF＝x，则AF＝，

由勾股定理得：DF2＝CD2－CF2，DF2＝AD2－AF2，

∴，

解得：，

∴OD＝2CF＝．