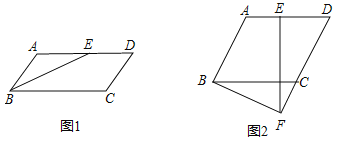题目内容
【题目】如图,点P为正方形ABCD的边CD上一点,BP的垂直平分线EF分别交BC、AD于E、F两点,GP⊥EP交AD于点G,连接BG交EF于点 H,下列结论:①BP=EF;②∠FHG=45°;③以BA为半径⊙B与GP相切;④若G为AD的中点,则DP=2CP.其中正确结论的序号是( )
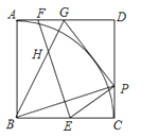
A. ①②③④ B. 只有①②③ C. 只有①②④ D. 只有①③④
【答案】A
【解析】
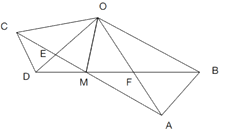
试题分析:结论①正确.如下图1:过点![]() 作
作![]() ,易用
,易用![]() 证
证![]() ,所以
,所以![]() ;结论②正确.如图2:过点
;结论②正确.如图2:过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,先利用同角的余角相等得
,先利用同角的余角相等得![]() ,继而证
,继而证![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,
,
在①的基础上易得出![]() ,所以
,所以![]() ;结论③正确,在②的基础上易得
;结论③正确,在②的基础上易得![]() ,即点
,即点![]() 到
到![]() 的距离等于⊙
的距离等于⊙![]() 的半径,所以⊙
的半径,所以⊙![]() 与
与![]() 相切;结论④正确,在②的基础上易得出
相切;结论④正确,在②的基础上易得出![]() ,
,![]() ,当
,当![]() 为
为![]() 的中点时,设
的中点时,设![]() ,
,![]() ;则
;则![]() ,
,![]() ,
,![]() .由勾股定理得:
.由勾股定理得:![]() ,即:
,即:![]() ,解得:
,解得:![]() ,所以
,所以![]()
即![]() ,故选
,故选![]() .
.


图1 图2

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目