题目内容
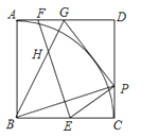
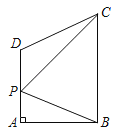
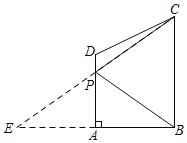
【题目】如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=4,点P是线段AD上的动点,连接BP,CP,若△BPC周长的最小值为16,则BC的长为( )
A.5B.6C.8D.10
【答案】B
【解析】
作点B关于AD的对称点E,连接CE交AD于P,则AE=AB=4,EP=BP,设BC=x,则CP+BP=16﹣x=CE,依据Rt△BCE中,EB2+BC2=CE2,即可得到82+x2=(16﹣x)2,进而得出BC的长.
解:如图所示,作点B关于AD的对称点E,连接CE交AD于P,则AE=AB=4,EP=BP,
设BC=x,则CP+BP=16﹣x=CE,
∵∠BAD=90°,AD∥BC,
∴∠ABC=90°,
∴Rt△BCE中,EB2+BC2=CE2,
∴82+x2=(16﹣x)2,
解得x=6,
∴BC=6,
故选:B.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目