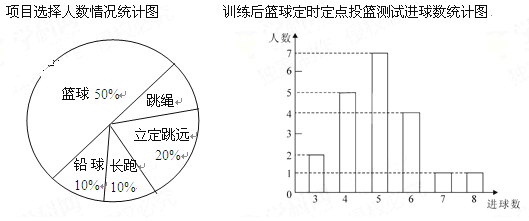
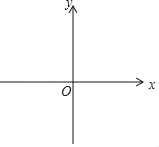
题目内容
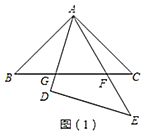
【题目】如图,在同一平面内,将两个全等的等腰直角三角形![]() 和
和![]() 摆放在一起,
摆放在一起,![]() 为公共顶点,
为公共顶点,![]() ,它们的斜边长为2,若
,它们的斜边长为2,若![]() 固定不动,
固定不动,![]() 绕点
绕点![]() 旋转,
旋转,![]() 、
、![]() 与边
与边![]() 的交点分别为
的交点分别为![]() 、
、![]() (点
(点![]() 不与点
不与点![]() 重合,点
重合,点![]() 不与点
不与点![]() 重合),设
重合),设![]() ,
,![]() .
.
(1)请在图(1)中找出两对相似但不全等的三角形,并选取其中一对进行证明.
(2)求![]() 与a的函数关系式,直接写出自变量a的取值范围.
与a的函数关系式,直接写出自变量a的取值范围.
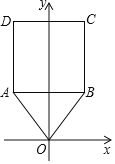
(3)以![]() 的斜边
的斜边![]() 所在的直线为
所在的直线为![]() 轴,
轴,![]() 边上的高所在的直线为
边上的高所在的直线为![]() 轴,建立平面直角坐标系如图(2),若
轴,建立平面直角坐标系如图(2),若![]() ,求出点
,求出点![]() 的坐标,猜想线段
的坐标,猜想线段![]() 、
、![]() 和
和![]() 之间的关系,并通过计算加以验证.
之间的关系,并通过计算加以验证.
【答案】(1)△ACG∽△FAG,△FAG∽△FBA,证明见解析;(2)b=![]() ,1<a<2;(3)G(1-
,1<a<2;(3)G(1-![]() ,0);BG2+CF2=FG2.
,0);BG2+CF2=FG2.
【解析】
(1)找到有公共角的和45°角的两个三角形即可;
(2)证明△ACG∽△FBA,利用相似三角形的对应边成比例可得![]() 与a的函数关系式,根据点F与点C重合时a为2,点G与点B重合时a为1,可得a的取值范围
与a的函数关系式,根据点F与点C重合时a为2,点G与点B重合时a为1,可得a的取值范围
(3)先求得a=b=![]() ,可求点G(1-
,可求点G(1-![]() ,0);根据BG=OB﹣OG,求得FG=BC﹣2BG=2
,0);根据BG=OB﹣OG,求得FG=BC﹣2BG=2![]() -2,即可得到线段
-2,即可得到线段![]() 、
、![]() 和
和![]() 之间的关系.
之间的关系.
(1)△ACG∽△FAG,△FAG∽△FBA.
∵∠GAF=∠C=45°,
∠AGF=∠AGC,
∴△ACG∽△FAG.类似证明△FAG∽△FBA;
(2)∵∠CAG=∠CAF+45°,∠BFA=∠CAF+45°,
∴∠CAG=∠BFA.
∵∠B=∠C=45°,
∴△ACG∽△FBA,
∴ ![]() =
=![]() .
.
由题意可得CA=BA=![]() .
.
∴![]() =
=![]() .∴b=
.∴b=![]() .
.
自变量a的取值范围为1<a<2.
(3)由BG=CF可得BF=CG,即a=b.
∵b=![]() ,
,
∴a=b=![]() .
.
∵OB=OC=![]() BC=1,
BC=1,
∴OF=OG=![]() ﹣1.
﹣1.
∴G(1-![]() ,0).
,0).
线段BG、FG和CF之间的关系为BG2+CF2=FG2;
∵BG=OB﹣OG=1-(![]() -1)=2-
-1)=2-![]() =CF,
=CF,
FG=BC﹣2BG= 2-2(2-![]() )=2
)=2![]() -2.
-2.
∵BG2+CF2=2(2-![]() )2=12-8
)2=12-8![]() ,FG2=(2
,FG2=(2![]() -2)2=12-8
-2)2=12-8![]() .
.
∴BG2+CF2=FG2 .

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案