题目内容
【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．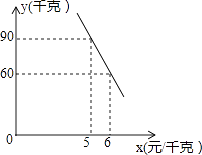 
（1）根据题意，填写如表：
（2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？
【答案】
（1）解：由题意知：当蔬菜批发量为60千克时：60×5=300（元），当蔬菜批发量为90千克时：90×5×0.8=360（元），
填写表格如下：
蔬菜的批发量（千克） | … | 25 | 60 | 75 | 90 | … |
所付的金额（元） | … | 125 | 300 | 300 | 360 | … |
蔬菜的批发量（千克） | … | 25 | 60 | 75 | 90 | … |
所付的金额（元） | … | 125 | 300 | 300 | 360 | … |
（2）解：设该一次函数解析式为y=kx+b（k≠0），
把点（5，90），（6，60）代入，得 
，
解得： 
．
故该一次函数解析式为：y=﹣30x+240；
（3）解：设当日可获利润w（元），日零售价为x元，由（2）知，
w=（﹣30x+240）（x﹣5×0.8）=﹣30（x﹣6）2+120，
∵﹣30x+240≥75，即x≤5.5，
∴当x=5.5时，当日可获得利润最大，最大利润为112.5元．
【解析】（1）根据这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元，可得60×5=300元；若超过60千克时，批发的这种蔬菜全部打八折，则90×5×0.8=360元；（2）把点（5，90），（6，60）代入函数解析式y=kx+b（k≠0），列出方程组，通过解方程组求得函数关系式；（3）利用最大利润=y（x﹣4），进而利用配方法求出函数最值即可．
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
【题目】某校合唱团有30名成员，下表是合唱团成员的年龄分布统计表：
年龄（单位：岁） | 13 | 14 | 15 | 16 |
频数（单位：名） | 5 | 15 | x | 10﹣x |
对于不同的x，下列关于年龄的统计量不会发生改变的是（ ）
A.平均数、中位数
B.平均数、方差
C.众数、中位数
D.众数、方差
