题目内容
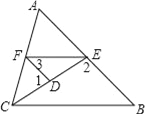
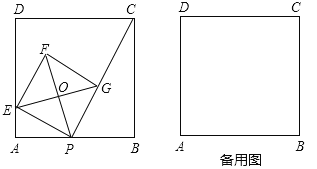
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() 是
是![]() 边上的一个动点,连接
边上的一个动点,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,顶点
,顶点![]() 在线段
在线段![]() 上,对角线
上,对角线![]() 、
、![]() 相交于点
相交于点![]() .(1)若
.(1)若![]() ,则
,则![]() ;
;
(2)①求证:点![]() 一定在
一定在![]() 的外接圆上;
的外接圆上;
②当点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,求点
也随之运动,求点![]() 经过的路径长;
经过的路径长;
(3)在点![]() 从点
从点![]() 到点
到点![]() 的运动过程中,
的运动过程中,![]() 的外接圆的圆心也随之运动,求该圆心到
的外接圆的圆心也随之运动,求该圆心到![]() 边的距离的最大值.
边的距离的最大值.
【答案】(1)![]() ;(2)①见解析;②2
;(2)①见解析;②2![]() ;(3)
;(3)![]() .
.
【解析】(1)根据正方形的性质得到∠A=∠B=∠EPG=90°,PF⊥EG,然后根据垂直的性质和直角三角形的两锐角互余的性质得到∠AEP=∠BPC,再根据两角对应相等的两三角形相似证得△APE∽△BCP,最后根据相似三角形的对应边成比例求解即可;
(2)①证明A、P、O、E四点共圆,即可得出结论;
②连接OA、AC,由勾股定理得到AC的长,由圆周角定理得出∠OAP=∠OEP=45°,点O在AC上,当点P运动到点B时,O为AC 的中点,即可求解;
(3)设△APE的外接圆的圆心为M,作MN⊥AB于N,由三角形中位线定理得到MN=![]() AE,设AP=x,则BP=4-x,由(1)中的相似三角形的性质:对应边成比例,求出AE= x-
AE,设AP=x,则BP=4-x,由(1)中的相似三角形的性质:对应边成比例,求出AE= x-![]() x2=-
x2=-![]() (x-2)2+1,由二次函数的最值求出AE的最大值为1,然后可求MN的值.
(x-2)2+1,由二次函数的最值求出AE的最大值为1,然后可求MN的值.
(1)解:∵四边形ABCD、四边形PEFG是正方形,
∴∠A=∠B=∠EPG=90°,PF⊥EG,AB=BC=4,∠OEP=45°,
∴∠AEP+∠APE=90°,∠BPC+∠APE=90°,
∴∠AEP=∠BPC,
∴△APE∽△BCP,
∴![]() ,即
,即![]() ,
,
解得:AE=![]() ;
;
(2)①证明:∵PF⊥EG,
∴∠EOP=90°,
∴∠EOP+∠A=180°,
∴A、P、O、E四点共圆,
∴点O一定在△APE的外接圆上;
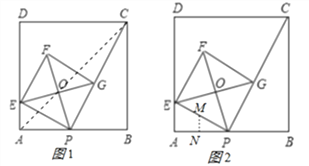
②解:连接OA、AC,如图1所示:
∵四边形ABCD是正方形,
∴∠B=90°,∠BAC=45°,
∴AC=![]() ,
,
∵A、P、O、E四点共圆,
∴∠OAP=∠OEP=45°,
∴点O在AC上,
当P运动到点B时,O为AC的中点,OA=![]() AC=2
AC=2![]() ,
,
即点O经过的路径长为2![]() ;
;
(3)解:设△APE的外接圆的圆心为M,作MN⊥AB于N,如图2所示:
则MN∥AE,
∵ME=MP,
∴AN=PN,
∴MN=![]() AE,
AE,
设AP=x,则BP=4-x,
由(1)得:△APE∽△BCP,
∴![]() ,即
,即![]() ,
,
解得:AE=x-![]() x2=-
x2=-![]() (x-2)2+1,
(x-2)2+1,
∴x=2时,AE的最大值为1,此时MN的值最大=![]() ×1=
×1=![]() ,即△APE的圆心到AB边的距离的最大值为
,即△APE的圆心到AB边的距离的最大值为![]() .
.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案