题目内容
【题目】如图，已知二次函数
（a≠0）的图像与x轴交于点A（-2,0）、B，与y轴交于点C，tan∠ABC=2．
（1）求抛物线的解析式及其顶点D的坐标；
（2）设直线CD交x轴于点E，过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF总有公共点．试探究：抛物线最多可以向上平移多少个单位长度？
（3）在线段OB的垂直平分线上是否存在点P，使得经过点P的直线PM垂直于直线CD，且与直线OP的夹角为75°？若存在，求出点P的坐标；若不存在，请说明理由；
【答案】(1) y=-(x-1)+9,(1,9);(2) 72个单位;(3)见解析.
【解析】（1）易知点C的坐标，那么在Rt△BOC中，根据tan∠ABC的值即可得到点B的坐标．然后利用待定系数法求出抛物线的解析式，通过对解析式进行配方能得到顶点D的坐标；
（2）首先确定直线CD的解析式以及点E的坐标，易得出△EOC是等腰直角三角形的结论，那么在四边形ENPM（以解答图为参考）中，根据四边形内角和可以求出∠OPN的度数，那么PN的长就可以在Rt△OPN中求出，以此求得点P的坐标；
（3）若抛物线向上平移，首先表示出平移后的函数解析式；当x=-8时（与点E横坐标相同），求出新函数的函数值，若抛物线与线段EF有公共点，那么该函数值应不大于点E的纵坐标．当x=4时（与点F的横坐标相同），方法同上，结合上述两种情况，即可得到函数图象的最大平移单位．
（1）由抛物线的解析式知，点C（0，8），即 OC=8；
Rt△OBC中，OB=OCtan∠ABC=8×
=4，则 点B（4，0）．
将A、B的坐标代入抛物线的解析式中，得：
，解得
，
∴抛物线的解析式：y=-x2+2x+8=-（x-1）2+9，顶点D（1，9）；
（2）设直线CD的解析式为：y=kx+8，
将点D坐标(1,9)代入上式，得：k=1；
∴直线CD：y=x+8，点E（-8，0），F（4，12）．
设抛物线向上平移m个单位长度（m＞0），则抛物线的解析式为：y=-（x-1）2+9+m；
当x=-8时，y=m-72，
当x=4时，y=m，
∴m-72≤0 或 m≤12，
∴0＜m≤72，
∴抛物线最多向上平移72个单位．
(3)存在符合条件的P点, 点E（-8，0）．
∴OC=OE=8，∠CEB=45°．
在四边形EMPN中（如图），∠MPN=180°-∠CEB=135°（∠PME、∠PNO都是直角），
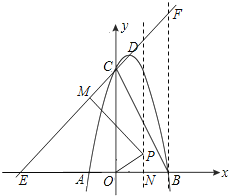
①当∠OPM=75°时，∠OPN=135°-75°=60°；
在Rt△OPN中，ON=OB=2，PN=
；
②当∠OPQ=75°时，∠OPN=135°+75°-180°=30°，
在Rt△OPN中，ON=OB=2，PN=2
；
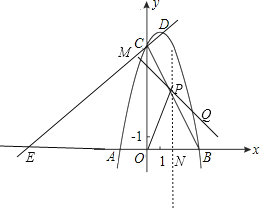
综上，存在符合条件的P点，且坐标为 （2，）或（2，2）.
