Question

已知函数y=-2x+6与函数y=3x-4．
（1）在同一平面直角坐标系内，画出这两个函数的图象；
（2）求这两个函数图象的交点坐标；
（3）根据图象回答，当x在什么范围内取值时，函数y=-2x+6的图象在函数y=3x-4的图象的上方？

Answer 1

分析：（1）可用两点法来画函数y=-2x+6与函数y=3x-4的图象；
（2）两函数相交，那么交点的坐标就是方程组

y=-2x+6 y=3x-4

的解；
（3）函数y=-2x+6的图象在函数y=3x-4的图象的上方，即-2x+6＞3x-4，解得x＜2．

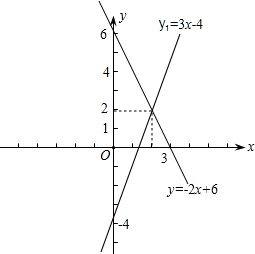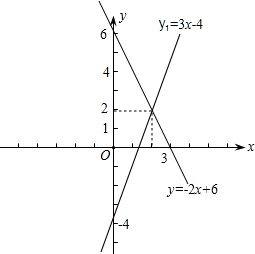解答：解：（1）函数y=-2x+6与坐标轴的交点为（0，6），（3，0）
函数y=3x-4与坐标轴的交点为（0，-4），（

4

3

，0）
作图为：

（2）解：根据题意得
方程组

y=-2x+6 y=3x-4

解得

x=2 y=2

即交点的坐标是（2，2）
∴两个函数图象的交点坐标为（2，2）

（3）由图象知，当x＜2时，函数y=-2x+6的图象在函数y=3x-4的图象上方．

点评：本题主要考查了一次函数的图象的画法及位置关系，难度不大．