题目内容
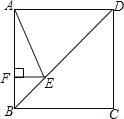
【题目】如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )
A. 4﹣2![]() B. 3
B. 3![]() ﹣4 C. 1 D.
﹣4 C. 1 D. ![]()
【答案】A
【解析】
根据正方形的对角线平分一组对角可得∠ABD=∠ADB=45°,再求出∠DAE的度数,根据三角形的内角和定理求∠AED,从而得到∠DAE=∠AED,再根据等角对等边的性质得到AD=DE,然后求出正方形的对角线BD,再求出BE,最后根据等腰直角三角形的直角边等于斜边的![]() 倍计算即可得解.
倍计算即可得解.
在正方形ABCD中,∠ABD=∠ADB=45°,
∵∠BAE=22.5°,
∴∠DAE=90°∠BAE=90°22.5°=67.5°,
在△ADE中,∠AED=180°45°67.5°=67.5°,
∴∠DAE=∠AED,
∴AD=DE=4,
∵正方形的边长为4,
∴BD=4![]() ,
,
∴BE=BDDE=4![]() 4,
4,
∵EF⊥AB,∠ABD=45°,
∴△BEF是等腰直角三角形,
∴EF=![]() BE=
BE=![]() ×(4
×(4![]() 4)=42
4)=42![]() .
.
故选A.

练习册系列答案
相关题目