题目内容
【题目】已知:如图所示,在平面直角坐标系![]() 中,
中,![]() .若点
.若点![]() 是边
是边![]() 上的一个动点(与点
上的一个动点(与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)当![]() 的周长与四边形
的周长与四边形![]() 的周长相等时,求
的周长相等时,求![]() 的长;
的长;
(3)在![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形?若存在,请求出此时
为等腰直角三角形?若存在,请求出此时![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.

【答案】(1)C(16,﹣12);(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
试题分析:(1)如图1,过C作CH⊥OB于H,根据勾股定理得到BC=![]() ,根据三角形的面积公式得到CH=
,根据三角形的面积公式得到CH=![]() ,由勾股定理得到OH=
,由勾股定理得到OH=![]() ,则得到结论;
,则得到结论;
(2)∵根据相似三角形的性质得到![]() ,设CM=x,则CN=
,设CM=x,则CN=![]() x,根据已知条件列方程即可得到结论;
x,根据已知条件列方程即可得到结论;
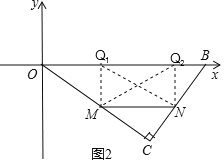
(3)如图2,由(2)知,当CM=x,则CN=![]() x,MN=
x,MN=![]() x,①当∠OMQ1=90°MN=MQ时,②当∠MNQ2=90°,MN=NQ2时,根据相似三角形的性质即可得到结论.
x,①当∠OMQ1=90°MN=MQ时,②当∠MNQ2=90°,MN=NQ2时,根据相似三角形的性质即可得到结论.
试题解析:(1)如图1,过C作CH⊥OB于H,

∵∠C=90°,OB=25,OC=20,∴BC=![]() ,
,
∵S△OBC=![]() OBCH=
OBCH=![]() OCBC,∴CH=
OCBC,∴CH=![]() ,
,
∴OH=![]() ,∴C(16,﹣12);
,∴C(16,﹣12);
(2)∵MN∥OB,∴△CNM∽△COB,∴![]() ,
,
设CM=x,则CN=![]() x,
x,
∵△MCN的周长与四边形OMNB的周长相等,
∴CM+CN+MN=OM+MN+OB,即x+![]() x+MN=20﹣x+mn+15﹣
x+MN=20﹣x+mn+15﹣![]() x+25,
x+25,
解得:x=![]() ,∴CM=
,∴CM=![]() ;
;
(3)如图2,由(2)知,当CM=x,则CN=![]() x,MN=
x,MN=![]() x,
x,
①当∠OMQ1=90°MN=MQ时,
∵△OMQ∽△OBC,∴![]() ,
,
∵MN=MQ,∴ ,∴x=
,∴x=![]() ,
,
∴MN=![]() x=
x=![]() ×
×![]() =
=![]() ;
;
②当∠MNQ2=90°,MN=NQ2时,
此时,四边形MNQ2Q1是正方形,
∴NQ2=MQ1=MN,∴MN=![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
