题目内容
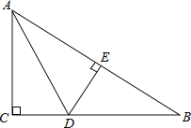
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的三条边逆时针走一圈回到
的三条边逆时针走一圈回到![]() 点,速度为2
点,速度为2![]() ,设运动时间为
,设运动时间为![]() 秒.
秒.
(1)![]() 时,
时,![]() 为等腰三角形?
为等腰三角形?
(2)另有一点![]() 从点
从点![]() 开始,按顺时针走一圈回到
开始,按顺时针走一圈回到![]() 点,且速度为每秒3cm,若
点,且速度为每秒3cm,若![]() 、
、![]() 两点同时出发,当
两点同时出发,当![]() 、
、![]() 中有一点到达终点时,另一点也停止运动.当
中有一点到达终点时,另一点也停止运动.当![]() 为何值时,直线
为何值时,直线![]() 把
把![]() 的周长分成相等的两部分?
的周长分成相等的两部分?

【答案】(1)t=8或6.5;(2)t=2.4或7.2
【解析】
(1)分情况讨论:①在边AB上时,有两种情况;②在边AB上时,不能构成三角形;③在边AC上时,不能构成三角形;
(2)分情况讨论:根据点P在BC、AB、AC边上讨论,根据周长平分列方程可得结论.
(1)①i当点P在AB上,如图,
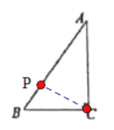
CA=AP时,AP=8,
则t=16÷2=8s,
①ii当点P在AB上,如图,
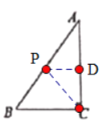
AP=CP时,过P作PD⊥AC于D,则AD=CD=![]() AC=4
AC=4
根据![]()
∴![]()
∴![]()
∴在Rt△PAC中,AP=![]() =5
=5
则t=13÷2=6.5s
故当t=8或6.5秒时,△ACP为等腰三角形;
(2)当P点在AC上,Q在AB上,PQ是相背运动,根据平分周长,则PQ运动的距离和是12,
∵直线PQ把△ABC的周长分成相等的两部分,
∴2t+3t=12,
∴t=2.4;
当P点在AB上,Q在AC上,相遇后是刚刚好合计走完一周,再次平分时又合计走了半周,
∵直线PQ把△ABC的周长分成相等的两部分,
∴2t+3t=36,
∴t=7.2,
∴当t=2.4或7.2秒时,直线PQ把△ABC的周长分成相等的两部分.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目