Question

【题目】如图，直线y=﹣x﹣4与抛物线y=ax2+bx+c相交于A，B两点，其中A，B两点的横坐标分别为﹣1和﹣4，且抛物线过原点．

（1）求抛物线的解析式；
（2）在坐标轴上是否存在点C，使△ABC为等腰三角形？若存在，求出点C的坐标，若不存在，请说明理由；
（3）若点P是线段AB上不与A，B重合的动点，过点P作PE∥OA，与抛物线第三象限的部分交于一点E，过点E作EG⊥x轴于点G，交AB于点F，若S△BGF=3S△EFP ， 求 的值．

Answer 1

【答案】
（1）

解：∵A，B两点在直线y=﹣x﹣4上，且横坐标分别为﹣1、﹣4，

∴A（﹣1，﹣3），B（﹣4，0），

∵抛物线过原点，

∴c=0，

把A、B两点坐标代入抛物线解析式可得 ，解得 ，

∴抛物线解析式为y=x2+4x

（2）

解：∵△ABC为等腰三角形，

∴有AB=AC、AB=BC和CA=CB三种情况，

①当AB=AC时，当点C在y轴上，设C（0，y），

则AB= =3 ，AC= ，

∴3 = ，解得y=﹣3﹣ 或y=﹣3+ ，

∴C（0，﹣3﹣ ）或（0，﹣3﹣ ）；

当点C在x轴上时，设C（x，0），则AC= ，

∴ =3 ，解得x=﹣4或x=2，当x=﹣4时，B、C重合，舍去，

∴C（2，0）；

②当AB=BC时，当点C在x轴上，设C（x，0），

则有AB=3 ，BC=|x+4|，

∴|x+4|=3 ，解得x=﹣4+3 或x=﹣4﹣3 ，

∴C（﹣4+3 ，0）或（﹣4﹣3 ，0）；

当点C在y轴上，设C（0，y），则BC= ，

∴ =3 ，解得y= 或y=﹣ ，

∴C（0， ）或（0，﹣ ）；

③当CB=CA时，则点C在线段AB的垂直平分线与y轴的交点处，

∵A（﹣1，﹣3），B（﹣4，0），

∴线段AB的中点坐标为（﹣ ，﹣ ），

设线段AB的垂直平分线的解析式为y=x+d，

∴﹣ =﹣ +d，解得d=1，

∴线段AB的垂直平分线的解析式为y=x+1，

令x=0可得y=1，令y=0可求得x=﹣1，

∴C（﹣1，0）或（0，1）；

综上可知存在满足条件的点C，其坐标为（0，﹣3﹣ ）或（0，﹣3﹣ ）或（﹣4+3 ，0）或（﹣4﹣3 ，0）或（﹣1，0）或（0，1）或（2，0）或（0， ）或（0，﹣ ）

（3）

解：过点P作PQ⊥EF，交EF于点Q，过点A作AD⊥x轴于点D，

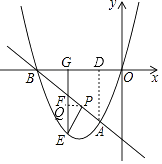
∵PE∥OA，GE∥AD，

∴∠OAD=∠PEG，∠PQE=∠ODA=90°，

∴△PQE∽△ODA，

∴ =3，即EQ=3PQ，

∵直线AB的解析式为y=﹣x﹣4，

∴∠ABO=45°=∠PFQ，

∴PQ=FQ，BG=GF，

∴EF=4PQ，

∴GE=GF+4PQ，

∵S△BGF=3S△EFP，

∴ GF2=3× 4PQ2，

∴GF=2 PQ，

∴ = =

【解析】（1）由直线解析式可分别求得A、B两点的坐标，利用待定系数法可求得抛物线解析式；（2）当AB=AC时，点C在y轴上，可表示出AC的长度，可求得其坐标；当AB=BC时，可知点C在x轴上，可表示出BC的长度，可求得其坐标；当AC=BC时点C在线段AB的垂直平分线与坐标轴的交点处，可求得线段AB的中点的坐标，可求得垂直平分线的解析式，则可求得C点坐标；（3）过点P作PQ⊥EF，交EF于点Q，过点A作AD⊥x轴于点D，可证明△PQE∽△ODA，可求得EQ=3PQ，再结合F点在直线AB上，可求得FQ=PQ，则可求得EF=4PQ，利用三角形的面积的关系可求得GF与PQ的关系，则可求得比值．