Question

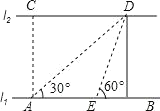
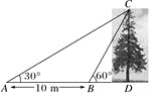
【题目】如图，某教学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10 m，到达B点，在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上)则这棵树CD的高度为( )

A. 10m B. 5m C. 5m D. 10m

Answer 1

【答案】C

【解析】

首先利用三角形的外角的性质求得∠ACB的度数，得到BC的长度，然后在直角△BDC中，利用三角函数即可求解．

解：∵∠CBD=60°，∠CBD=∠A+∠ACB，
∴∠ACB=∠CBD-∠A=60°-30°=30°，
∵∠A=30°，
∴∠A=∠ACB，
∵AB=10，
∴BC=AB=10，
在R△BCD中，CD=BCsin∠CBD=10×=5m
故选：C．