题目内容
已知:点P为正方形ABCD内部一点,且∠BPC=90°,过点P的直线分别交边AB、边CD于点E、点F.
(1)如图1,当PC=PB时,则S△PBE、S△PCF S△BPC之间的数量关系为 _________ ;
(2)如图2,当PC=2PB时,求证:16S△PBE+S△PCF=4S△BPG;
(3)在(2)的条件下,Q为AD边上一点,且∠PQF=90°,连接BD,BD交QF于点N,若S△bpc=80,BE=6.求线段DN的长.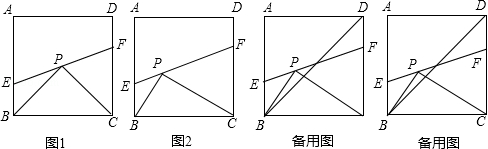
(1)如图1,当PC=PB时,则S△PBE、S△PCF S△BPC之间的数量关系为 _________ ;
(2)如图2,当PC=2PB时,求证:16S△PBE+S△PCF=4S△BPG;
(3)在(2)的条件下,Q为AD边上一点,且∠PQF=90°,连接BD,BD交QF于点N,若S△bpc=80,BE=6.求线段DN的长.

(1)S△PBE+S△PCF=S△BPC; (2)见解析 (3)DN=2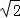 或3
或3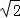
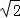 或3
或3
试题分析:(1)如图1所示:过点P作PI⊥BC于点I,
∵PB=PC,
∴PI∥BE∥CF,
∴PI是梯形BCFE的中位线,
∴PI=
 (BE+CF),
(BE+CF),∵△PBC是等腰直角三角形,
∴PI=AB=CI,
∴S△PBE+S△PCF=
 BE•BI+
BE•BI+ CF•CI=
CF•CI= BE×
BE× BC+
BC+ CF•
CF• BC=
BC= BC(BE+CF)=
BC(BE+CF)= BC•PI=S△PBC;
BC•PI=S△PBC;故答案为:S△PBE+S△PCF=S△BPC;
(2)如图2,过点P作PG⊥EF交BC于点G,∠EPG=90°,
∵∠BPC=90°,
∴∠EPB+∠BPG=90°,
∵∠BPG+∠CPG=90°,
∴∠EPB=∠CPG,
同理,∵∠EBP+∠PBC=90°,∠PBC+∠BCP=90°,
∴∠EBP=∠BCP,
∴△EPB∽△GPC,
∵PC=2PB,
∴
 =(
=(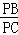 )2=
)2=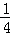
∴S△GPC=4S△EPB,
同理可得S△FPC=4S△GPB,
∵S△PBG+S△PGC=S△BPC,
∴16S△PBE+S△PFC=4S△BPC;
(3)如图3,设正方形的边长为a(a>0),
∵∠BPC=90°,PC=2PB,S△BPC=80,
∴
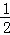 •
• •
•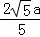 =80,解得a=20,
=80,解得a=20,由(2)知,△EPB∽△GPC,
∴CG=2BE=12,
∴BG=8,
∴CF=16,DF=4,
过点P作PM∥AB交BC于点M.交AD于点H,过点P作PT⊥CD于T,
∵PM⊥BC,BC=20,S△BPC=80,
∴PM=8,
∴PH=12,PT=16,FT=8,
∵∠PQF=90°,
∴由勾股定理得,(HQ2+HP2)+(DQ2+DF2)=PT2+TF2,即(16﹣DQ)2+122+(DQ2+42)=162+82,解得DQ=4或DQ=12,
当DQ=4时,
∵DQ=DF=4,∠PQF=90°,DN为∠QDF的角平分线,
∴DN=
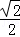 QD=2
QD=2 ;
;当DQ=12时,过点N作NN1⊥QD于N1,
∵∠QOF=90°,DN为∠QDF的角平分线,
∴∠QDN=45°,
∵NN1⊥AD,
∴NN1=N1D,△QDF∽△QN1N,
∴
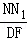 =
= ,
, =
=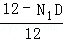 ,解得NN1=3,
,解得NN1=3,∴DN=
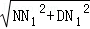 =
=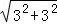 =3
=3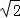 ,
,综上所述,DN=2
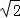 或3
或3 .
.
点评:本题考查的是相似形的综合题,涉及到相似三角形的判定与性质、正方形的性质、等腰三角形的性质及勾股定理,解答此题的关键是作出辅助线,构造出相似三角形,再利用相似三角形的性质进行解答.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
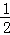 ,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.
,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.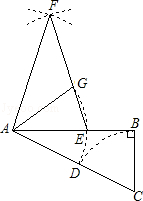

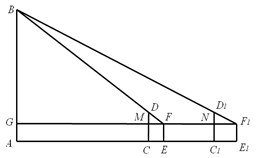

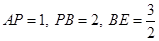 ,试求出AD的长.
,试求出AD的长. 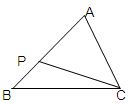

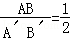 ,AB边上的中线CD=4cm,△ABC的周长为20cm,△A′B′C′的面积是64cm2,求:
,AB边上的中线CD=4cm,△ABC的周长为20cm,△A′B′C′的面积是64cm2,求: