题目内容
【题目】如图,正方形![]() 的边长为4,在这个正方形内作等边三角形
的边长为4,在这个正方形内作等边三角形![]() (三角形的顶点可以在正方形的边上),使它们的中心重合,则
(三角形的顶点可以在正方形的边上),使它们的中心重合,则![]() 的顶点到正方形
的顶点到正方形![]() 的顶点的最短距离是___________.
的顶点的最短距离是___________.

【答案】![]()
【解析】
当G,O,C共线时,△EFG的顶点到正方形ABCD的顶点的最短,即点G在对角线上,在△AOE中,∠CAE=45°,∠AOE=60°,OE=r,解三角形可求r,即可求最短距离.
如图:当G,O,C共线时,△EFG的顶点到正方形ABCD的顶点的最短,即点G在对角线上.
作EM⊥AC于M
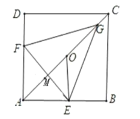
∵ABCD是正方形,AB=4
∴AC=![]() ,AO=
,AO=![]() ,∠CAB=45°
,∠CAB=45°
∵△EFG是等边三角形
∴∠GOE=120°
∴∠AOE=60°
设OE为r
∵∠AOE=60°,ME⊥AO
∴MO=![]() OE=
OE=![]() r,ME=
r,ME=![]() MO=
MO=![]() r
r
∵∠MAE=45°,AM⊥ME
∴∠MAE=∠MEA=45°,
∴AM=ME=![]() r,
r,
∵AM+MO=AO
∴![]() r+
r+![]() r=
r=![]()
∴r=![]()
∵AG=AM=MO+OG=![]() r+
r+![]() r+r=
r+r=![]()
∴GC=![]()
故答案为:![]() .
.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
【题目】在倡导“社会主义核心价值观”演讲比赛中,某校根据初赛成绩在七、八年级分别选出10名同学参加决赛,对这些同学的决赛成绩进行整理分析,绘制成如下团体成绩统计表和选手成绩折线统计图:
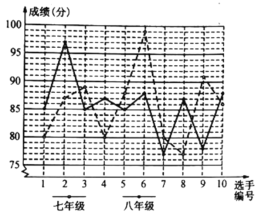
七年级 | 八年级 | |
平均数 | 85.7 | _______ |
众数 | _______ | _______ |
方差 | 37.4 | 27.8 |
根据上述图表提供的信息,解答下列问题:
(1)请你把上面的表格填写完整;
(2)考虑平均数与方差,你认为哪个年级的团体成绩更好?
(3)假设在每个年级的决赛选手中分别选出2个参加决赛,你认为哪个年级的实力更强一些?请说明理由.