题目内容
【题目】已知圆O的直径为4cm,A是圆上一固定点,弦BC的长为2![]() cm,当△ABC为等腰三角形时,其底边上的高为_____.
cm,当△ABC为等腰三角形时,其底边上的高为_____.
【答案】![]() 或2,或
或2,或![]()
【解析】
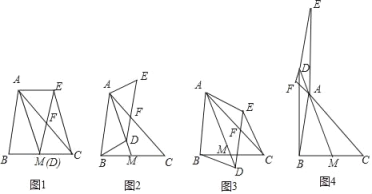
当BC为底边时,如图1,连接AO延长与BC交于F,由全等三角形的判定定理得△ABO≌△ACO,∠BAO=∠CAO,得△ABF≌△ACF,由全等的性质得,BF=CF,由垂径定理得,AF⊥BC,AF为△ABC的高,利用勾股定理可得OF,可得AF的长;
当BC为腰时,如图2,连接BO并延长与AC交于F,由全等三角形的判定定理得△ABO≌△CBO,∠ABO=∠CBO,得△ABF≌△CBF,由全等的性质得,AF=CF,由垂径定理得,BF⊥AC,BF为△ABC的高,由勾股定理逆定理得,△BOC为等腰直角三角形,∠CBO=45°,由等腰三角形的性质得,BF=CF,利用勾股定理可得BF的长;
当如图3所示时,BC为底,利用垂径定理得BF=CF=![]() ,利用勾股定理可得AF的长.
,利用勾股定理可得AF的长.
解:当BC为底边时,如图1,连接AO延长与BC交于F,

在△ABO与△ACO中,

∴△ABO≌△ACO(SSS),
∴∠BAO=∠CAO,
在△ABF与△ACF中,

∴△ABF≌△ACF(SAS),
∴BF=CF=![]() ,
,
∴AF⊥BC,
∴AF为△ABC的高,
在直角△BOF中,
OF=![]() =
=![]() =
=![]() ,
,
∴AF=2+![]() ;
;
当BC为腰时,如图2,连接BO并延长与AC交于F,
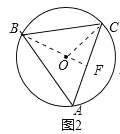
同理可证得:△ABO≌△CBO,
∴∠ABO=∠CBO,
可得△ABF≌△CBF,
∴AF=CF,
∴BF⊥AC,BF为△ABC的高,
∵OB2+OC2=8,BC2=8,
∴△BOC为等腰直角三角形,
∴∠CBO=45°,
∴CF=BF,
设CF=BF=x,
则2x2=8,
解得:x=2,
∴BF=2,
当如图3所示时,BC为底,
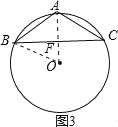
∵AF⊥BC,
∴BF=CF=![]() ,
,
设AF=x,则OF=2﹣x,
∴(2﹣x)2+(![]() )2=22,
)2=22,
解得:x=2+![]() 或x=2-
或x=2-![]()
故答案为:2+![]() 或2或2-
或2或2-![]() .
.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案