题目内容
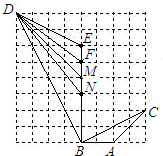 如图,在正方形网格上,与△ABC相似的三角形是( )
如图,在正方形网格上,与△ABC相似的三角形是( )| A、△NBD | B、△MBD | C、△EBD | D、△FBD |
分析:根据正方形的小格可以发现∠BAC=90°+45°=135°,
=
,所以和它相似的三角形也应该有一个钝角是135°,夹钝角的两边比是
,根据这一特点进行选择.
| AC |
| AB |
| 2 |
| 2 |
解答:解:∵在△ABC中,∠BAC=90°+45°=135°,
=
,
∠BMD=135°,
=
,
∴△MBD∽△ABC.
故选B.
| AC |
| AB |
| 2 |
∠BMD=135°,
| MD |
| BM |
| 2 |
∴△MBD∽△ABC.
故选B.
点评:此类题要首先找到已知三角形的特点,再根据相似三角形的判定进行观察选择.

练习册系列答案
相关题目
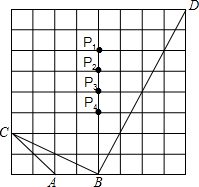 如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.
如图,在正方形网格上,若使△ABC∽△PBD,则点P应在( )处.| A、P1 | B、P2 | C、P3 | D、P4 |
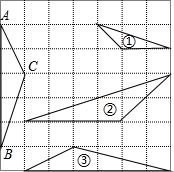 如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有
如图,在正方形网格上的三角形①,②,③中,与△ABC相似的三角形有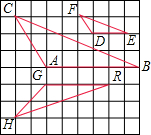 如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是
如图,在正方形网格上有三个三角形,则与△FDE相似的三角形是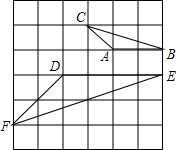 如图,在正方形网格上有△ABC和△DEF.
如图,在正方形网格上有△ABC和△DEF.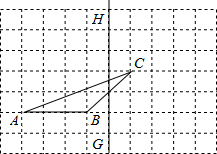 作图计算题.
作图计算题.