题目内容

如图所示，△ABC为直角三角形，∠ACB=90°， BF平分∠ABC，CD⊥AB于D，CD交BF于点G，GE∥CA，求证：CE与FG互相垂直平分。
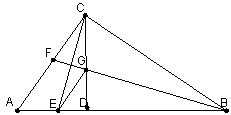
证明：连接EF     
∵BF平分∠ABC      ∴∠CBF=∠DBG       
在Rt△FCB和Rt△GDB中     
∠CFB=∠DGB=∠FGC       ∴CF=CG   
又∵ GE‖CA      ∴ ∠CFG=∠FGE=∠CGF     
∴∠CGB=∠EGB     
在△CGB和△EGB中        
GB=GB    ∠CGB=∠EGB     ∠CBG=∠DBG       
∴△CGB≌△EGB    CG=EG=FC     
∴ 四边形CFEG是菱形
∴ 对角线CE与FG互相垂直平分。
练习册系列答案
相关题目
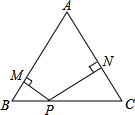如图所示，△ABC为等边三角形，D、E分别是CB、BC延长线上的点，连接AD、AE，且∠D精英家教网AE=120°，试问：
（1）△ADB与△EDA能相似吗？
（2）△ADB与△EAC能相似吗？
（3）BC2=BD•CE能成立吗？请说明以上各问的理由．
精英家教网如图所示，△ABC为正三角形，P是BC上的一点，PM⊥AB，PN⊥AC，设四边形AMPN，△ABC的周长分别为m、n，则有（　　）
A、
1
2
＜
m
n
＜
3
5
B、
2
3
＜
m
n
＜
3
4
C、80%＜
m
n
＜83%
D、78%＜
m
n
＜79%
附加题．观察计算
当a=5，b=3时，
a+b
2
与
ab
的大小关系是
＞
＞
．
当a=4，b=4时，
a+b
2
与
ab
的大小关系是
=
=
．
●探究证明
如图所示，△ABC为圆O的内接三角形，AB为直径，过C作CD⊥AB于D，设AD=a，BD=b．
（1）分别用a，b表示线段OC，CD；
（2）探求OC与CD表达式之间存在的关系（用含a，b的式子表示）．
●归纳结论
根据上面的观察计算、探究证明，你能得出
a+b
2
与
ab
的大小关系是：
a+b
2
≥
ab
（当a=b时，取“=”）
a+b
2
≥
ab
（当a=b时，取“=”）
．
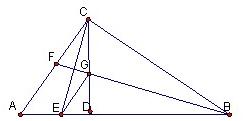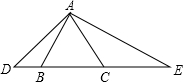
如图所示，△ABC为直角三角形，∠ACB=90°，BF平分∠ABC，CD⊥AB于D，CD交BF于点G，GE∥CA，求证：CE与FG互相垂直平分．
如图所示的△ABC为等边三角形，边长为2，D为BC中点，△ADC绕点A顺时针旋转60°得到△AEB，则BE=
1
1
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网