题目内容
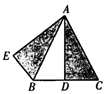
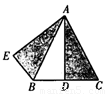
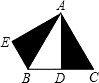
 如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=
如图所示的△ABC为等边三角形,边长为2,D为BC中点,△ADC绕点A顺时针旋转60°得到△AEB,则BE=1
1
.分析:根据等边三角形的性质得到DC=1,∠CAB=60°,CA=BA,由于△ADC绕点A顺时针旋转60°得到△AEB,则AC旋转到AB,AD旋转到AE,DC旋转到BE,根据旋转的性质即可得到BE=DC=1.
解答:解:∵△ABC为等边三角形,边长为2,D为BC中点,
∴DC=1,∠CAB=60°,CA=BA,
∵△ADC绕点A顺时针旋转60°得到△AEB,
∴AC旋转到AB,AD旋转到AE,DC旋转到BE,
∴BE=DC=1.
故答案为1.
∴DC=1,∠CAB=60°,CA=BA,
∵△ADC绕点A顺时针旋转60°得到△AEB,
∴AC旋转到AB,AD旋转到AE,DC旋转到BE,
∴BE=DC=1.
故答案为1.
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.也考查了等边三角形的性质.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目