题目内容
【题目】如图，正方形ABCD的边长为4，点P为对角线BD上一动点，点E在射线BC上．
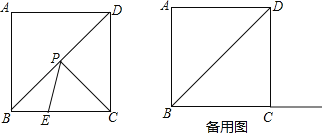
（1）填空：∠PBC= 度．
（2）若BE=t，连结PE、PC，则|PE+PC的最小值为 ，|PE﹣PC|的最大值是 （用含t的代数式表示）；
（3）若点E 是直线AP与射线BC的交点，当△PCE为等腰三角形时，求∠PEC的度数．
【答案】（1）45；（2）
；|4﹣t|；（3）当△PCE为等腰三角形时，∠PEC的度数为30°或120°．
【解析】
试题分析：（1）根据正方形的对角线平分一组对角，且四个角为直角，确定出所求角度数即可；
（2）连接AP，当AP与PE在一条线上时，PE+PC最小，利用勾股定理求出最小值；当P与B重合时，|PE﹣PC|最大，表示出最大值即可；
（3）分两种情况考虑：①当E在BC延长线上时，如图2所示，△PCE为等腰三角形，则CP=CE；②当E在BC上，如图3所示，△PCE是等腰三角形，则PE=CE，分别求出∠PEC的度数即可．
解：（1）∠PBC=45度；
故答案为：45；
（2）如图1所示：当AP与PE在一条线上时，PE+PC最小，
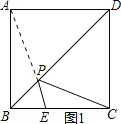
∵AB=4，BE=t，
∴PE+PC的最小值为；
当P与B重合时，|PE﹣PC|的最大值，最大值是|4﹣t|；
故答案为：；|4﹣t|；
（3）分两种情况考虑：
①当点E在BC的延长线上时，
如图2所示，△PCE是等腰三角形，则CP=CE，
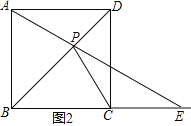
∴∠CPE=∠CEP，
∴∠BCP=∠CPE+∠CEP=2∠CEP，
∵在正方形ABCD中，∠ABC=90°，
∴∠PBA=∠PBC=45°，
在△ABP和△CBP中，
，
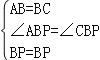∴△ABP≌△CBP（SAS），
∴∠BAP=∠BCP=2∠CEP，
∵∠BAP+∠PEC=90°，
∴2∠PEC+∠PEC=90°，
∴∠PEC=30°；
②当点E在BC上时，
如图3所示，△PCE是等腰三角形，则PE=CE，
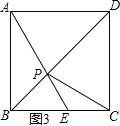
∴∠CPE=∠PCE，
∴∠BEP=∠CPE+∠PCE=2∠ECP，
∵四边形ABCD是正方形，
∴∠PBA=∠PBC=45°，
又AB=BC，BP=BP，
∴△ABP≌△CBP，
∴∠BAP=∠BCP，
∵∠BAP+∠AEB=90°，
∴2∠BCP+∠BCP=90°，
∴∠BCP=30°，
∴∠AEB=60°，
∴∠PEC=180°﹣∠AEB=120°，
综上所述：当△PCE为等腰三角形时，∠PEC的度数为30°或120°．
