题目内容
(本题满分10分)如图,直线y=kx-1与x轴、y轴分别交与B、C两点,tan∠OCB=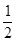 .
.
(1) 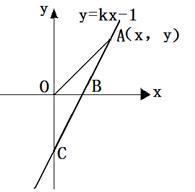 求B点的坐标和k的值;
求B点的坐标和k的值;
(2) 若点A(x,y)是第一象限内的直线y=kx-1上的一个动点.当点A运动过程中,试写出△AOB的面积S与x的函数关系式;
(3) 探索:
①当点A运动到什么位置时,△AOB的面积是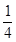 ;
;
②在①成立的情况下,x轴上是否存在一点P,使△POA是等腰三角形.若存在,请写出满足条件的所有P点的坐标;若不存在,请说明理由.
【答案】
(1)∵y= kx-1与y轴相交于点C,
∴OC=1 ∵tan∠OCB=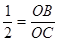
∴OB=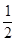 ∴B点坐标为:
∴B点坐标为: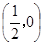 ,---------------------1分
,---------------------1分
把B点坐标为: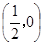 代入y= kx-1得 k=2---------------------2分
代入y= kx-1得 k=2---------------------2分
(2)∵S = 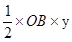 ∵y=2x-1 ∴S =
∵y=2x-1 ∴S =
∴S =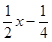 ---------------------4分
---------------------4分
(3)①当S =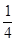 时,
时,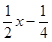 =
=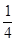 ∴x=1,y=2x-1=1
∴x=1,y=2x-1=1
∴A点坐标为(1,1)时,△AOB的面积为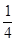 ----------------------------6分
----------------------------6分
②存在.
满足条件的所有P点坐标为:P1(1,0), P2(2,0), P3(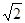 ,0),
P4(
,0),
P4(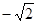 ,0). -----10分
,0). -----10分
【解析】
此题是典型的数形结合,既有函数思想,又有几何知识,综合性较强。

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目

 的图象的顶点为
的图象的顶点为 .二次函数
.二次函数 的图象与
的图象与 轴交于原点
轴交于原点 及另一点
及另一点 ,它的顶点
,它的顶点 在函数
在函数
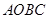 为菱形时,求函数
为菱形时,求函数 与支架
与支架 所在直线相交于水箱横断面
所在直线相交于水箱横断面 的圆心
的圆心 ,支架
,支架 垂直,
垂直, 厘米,
厘米,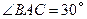 ,另一根辅助支架
,另一根辅助支架 厘米,
厘米, .
. 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据: )
)


