题目内容
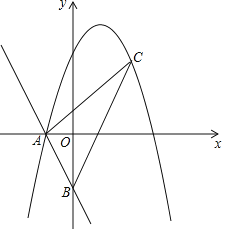
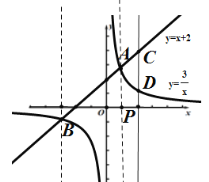
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与函数
与函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)已知点![]() ,过点
,过点![]() 作平行于
作平行于![]() 轴的直线,交直线
轴的直线,交直线![]() 于点
于点![]() ,交函数
,交函数![]() 的图象于点
的图象于点![]() .
.
①当![]() 时,求线段
时,求线段![]() 的长;
的长;
②若![]() ,结合函数的图象,直接写出
,结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() 或
或![]()
【解析】
(1)先把点A代入一次函数得到a的值,再把点A代入反比例函数,即可求出k;
(2)①根据题意,先求出m的值,然后求出点C、D的坐标,即可求出CD的长度;
②根据题意,当PC=PD时,点C、D恰好与点A、B重合,然后求出点B的坐标,结合函数图像,即可得到m的取值范围.
解:(1)把![]() 代入
代入![]() ,得
,得![]() ,
,
∴点A为(1,3),
把![]() 代入
代入![]() ,得
,得![]() ;
;
(2)当![]() 时,点P为(2,0),如图:
时,点P为(2,0),如图:
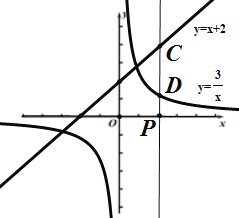
把![]() 代入直线
代入直线![]() ,得:
,得:![]() ,
,
∴点C坐标为(2,4),
把![]() 代入
代入![]() ,得:
,得:![]() ,
,
∴![]() ;
;
②根据题意,当PC=PD时,点C、D恰好与点A、B重合,如图,
∵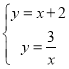 ,解得:
,解得:![]() 或
或![]() (即点A),
(即点A),
∴点B的坐标为(![]() ),
),
由图像可知,当![]() 时,有
时,有
点P在![]() 的左边,或点P在
的左边,或点P在![]() 的右边取到,
的右边取到,
∴![]() 或
或![]() .
.

练习册系列答案
相关题目