题目内容
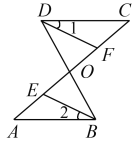
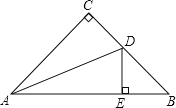
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)判断四边形ABDF的形状,并说明理由;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
【答案】(1)详见解析;(2)详见解析;(3)10.
【解析】
(1)根据平行线的性质和中线的性质,得出△AFE≌△DBE,即可解答.;
(2)由D是BC的中点,可得CD=AF,证得四边形ADCF是平行四边形,继而判定四边形ADCF是菱形;
(3)根据题意得四边形ABDF是平行四边形,即可求得DF的长,然后由菱形的面积等于其对角线积的一半,求得答案.
(1)解:四边形ABDF是平行四边形.
∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
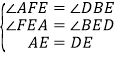
∴△AFE≌△DBE(AAS);
∴AF=DB.又∵AF∥BC
∴四边形ABDF是平行四边形

(2)证明:∵DB=DC,
∴AF=CD,
又∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形;
(3)解:∵四边形ABDF是平行四边形,
∴DF=AB=5,
∵四边形ADCF是菱形,
∴S=![]() ACDF=10.
ACDF=10.

【题目】为拓展学生视野,促进书本知识与生活实践的深度融合,荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每位老师带队14名学生,则还剩10名学生没老师带;若每位老师带队15名学生,就有一位老师少带6名学生,现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 | 乙型客车 | |
载客量(人/辆) | 35 | 30 |
租金(元/辆) | 400 | 320 |
学校计划此次研学活动的租金总费用不超过3000元,为安全起见,每辆客车上至少要有2名老师.
(1)参加此次研学活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师,可知租车总辆数为 辆;
(3)学校共有几种租车方案?最少租车费用是多少?