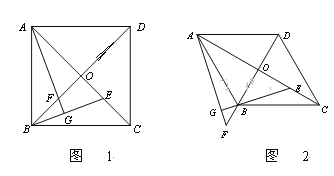
��Ŀ����
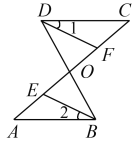
����Ŀ�������ϵ�A��Ӧ����Ϊa����B��Ӧ����Ϊb���Ҷ���ʽ6x3y��2xy��5�Ķ�����ϵ��Ϊa��������Ϊb
(1) ֱ��д����a��__________��b��_________
(2) �����ϵ�P��Ӧ����Ϊx����PA��PB��20����x��ֵ
(3) ����M�ӵ�A��������ÿ��1����λ���ȵ��ٶ������������ƶ���ͬʱ��N�ӵ�B��������ÿ��2����λ���ȵ��ٶ������������ƶ�������A����������ز����Ҽ����ƶ������������M��N�������1����λ����
���𰸡���1����1��a����2��b��5����2��x����8.5��11.5����3��2���![]() ���6���8��
���6���8��
��������
��1�����ݶ���ʽ��ϵ�����ɵó����ۣ�
��2����������ۣ�����P�ڵ�A���ʱ������P�ڵ�A�ұ�ʱ���ڵ�B��ߣ��Լ�����P�ڵ�B�ұ�ʱ����������ֱ���⼴�� ��
��3���ֵ�Nδ�����A֮ǰ��֮����������⼴�ɵó����ۣ�
��1���߶���ʽ6x3y-2xy+5�Ķ�����ϵ��Ϊa��������Ϊb��
��a=-2��b=5��
�ʴ�Ϊ��-2��5��
��2���ٵ���P�ڵ�A�������PA+PB=20��: (��2 ��x )+(5��x)=20, ��![]()
�ڵ���P�ڵ�A�ұߣ��ڵ�B�������PA+PB=20��: x ������2 ��+(5��x)=20,
��![]() ��������
��������
�۵���P�ڵ�B�ұ�����PA+PB=20��:x ������2 ��+(x��5), ��![]() .
.
��![]() ��11.5��
��11.5��
��3���辭��t���M��N�������1����λ���ȣ�
���˶�֪��AM��t��BN��2t��
�� ����N�����A֮ǰʱ��
��M��N����ǰ��M��N�������1����λ���ȣ�
t��1��2t��5��2��
���ԣ�t��2�룬
��M��N������M��N�������1����λ���ȣ�
t��2t��1��5��2��
���ԣ�t��![]() �룬
�룬
�� ����N�����A֮��ʱ��
��Nδ��Mʱ��M��N�������1����λ���ȣ�
t��[2t����5��2��]��1��
���ԣ�t��6�룻
��N��M��ʱ��M��N�������1����λ���ȣ�
[2t����5��2��]��t��1��
���ԣ�t��8�룻
��������2���![]() ���6���8���M��N�������1����λ���ȣ�
���6���8���M��N�������1����λ���ȣ�

 ѧ���������ν��Ͼ���ѧ������ϵ�д�
ѧ���������ν��Ͼ���ѧ������ϵ�д� Happy holiday���ּ��������ҵ�㶫���������ϵ�д�
Happy holiday���ּ��������ҵ�㶫���������ϵ�д�����Ŀ��Ϊ��չѧ����Ұ���ٽ��鱾֪ʶ������ʵ��������ںϣ�������ij��ѧ��֯���꼶ȫ��ѧ��ǰ�����̛�ˮ��ѧ���ؿ�չ��ѧ����ڴ˴λ�У���ÿλ��ʦ����14��ѧ������ʣ10��ѧ��û��ʦ������ÿλ��ʦ����15��ѧ��������һλ��ʦ�ٴ�6��ѧ�������мס������ִ��Ϳͳ������ǵ��ؿ�������������ʾ��
���Ϳͳ� | ���Ϳͳ� | |
�ؿ�������/���� | 35 | 30 |
���Ԫ/���� | 400 | 320 |
ѧУ�ƻ��˴���ѧ�������ܷ��ò�����3000Ԫ��Ϊ��ȫ�����ÿ���ͳ�������Ҫ��2����ʦ��
��1���μӴ˴���ѧ�����ʦ��ѧ�����ж����ˣ�
��2����Ҫ��֤����ʦ�����г�������Ҫ��֤ÿ����������Ҫ��2����ʦ����֪�������Ϊ�� ������
��3��ѧУ���м��������������������Ƕ��٣�