题目内容
已知正比例函数y=kx(k≠0)与反比例函数y=| m |
| x |
(1)求正比例函数及反比例函数的解析式;
(2)在所给的平面直角坐标系中画出两个函数的图象,根据图象直接写出点B的坐标及不等式kx>
| m |
| x |
分析:(1)把点A的坐标(2,3)分别代入y=kx(k≠0)与y=
(m≠0),即可求出正比例函数及反比例函数的解析式;
(2)根据函数的解析式及其图象特征分别画出它们的图象,它们在第三象限内的交点坐标即为点B的坐标;求不等式kx>
的解集,即求直线位于双曲线的上方时,对应的自变量x的取值范围.
| m |
| x |
(2)根据函数的解析式及其图象特征分别画出它们的图象,它们在第三象限内的交点坐标即为点B的坐标;求不等式kx>
| m |
| x |
解答: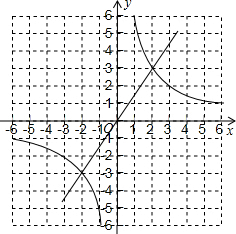 解:(1)∵点A(2,3)在正比例函数y=kx的图象上,
解:(1)∵点A(2,3)在正比例函数y=kx的图象上,
∴2k=3,
解得:k=
.
∴正比例函数的解析式为y=
x;
∵点A(2,3)在反比例函数y=
的图象上,
∴
=3,
解得:m=6.
∴反比例函数的解析式为y=
.
(2)根据图象,可知点B的坐标为(-2,-3);
∵当-2<x<0或x>2时,直线y=kx的图象在y=
图象的上方,
∴不等式kx>
的解集为-2<x<0或x>2.
 解:(1)∵点A(2,3)在正比例函数y=kx的图象上,
解:(1)∵点A(2,3)在正比例函数y=kx的图象上,∴2k=3,
解得:k=
| 3 |
| 2 |
∴正比例函数的解析式为y=
| 3 |
| 2 |
∵点A(2,3)在反比例函数y=
| m |
| x |
∴
| m |
| 2 |
解得:m=6.
∴反比例函数的解析式为y=
| 6 |
| x |
(2)根据图象,可知点B的坐标为(-2,-3);
∵当-2<x<0或x>2时,直线y=kx的图象在y=
| m |
| x |
∴不等式kx>
| m |
| x |
点评:本题主要考查了待定系数法求反比例函数与一次函数的解析式,同时体现了数形结合的思想.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2,-1),则它的另一个交点的坐标是( )
| k2 |
| x |
| A、(2,1) |
| B、(-2,-1) |
| C、(-2,1) |
| D、(2,-1) |
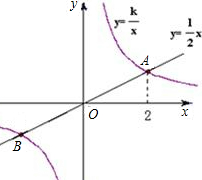 横坐标为2.
横坐标为2. 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).